Доли сложить калькулятор: Онлайн калькулятор: Дроби

Калькулятор онлайн — Калькулятор дробей

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель,

Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а знаменатель п — делитель:
\( m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.

Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)

Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)

Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.

Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).

Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.

Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).

С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)

Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

Инженерный калькулятор онлайн KALKPRO.RU — самый точный калькулятор корней, степеней, синусов, косинусов, логарифмов!

Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.

Только корректные расчеты по всем правилам математики!

В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.

Всё для вашего удобства:

• быстрые вычисления и загрузка,
• верные расчеты по всем правилам,
• полный функционал,
• понятный интерфейс,
• адаптация под любой размер устройства
• бесплатно
• не надо ничего устанавливать,
• никакой всплывающей назойливой рекламы,
• подробная инструкция с примерами

Содержание справки:

1. Комплекс операций инженерного калькулятора

2. Инструкция по функциям инженерного калькулятора

3. Как пользоваться инженерным калькулятором – на примерах

4. Тригонометрический калькулятор онлайн — примеры

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только. y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 [x^y] 6 [=]

Ответ: сорок пять в шестой степ. равно 8303765625

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90 [sin] [=]

Ответ: единица

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60 [cos] [=]

Решение: 0,5

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 [Deg] [=] 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1 [log] [=]

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100 [log] [=]

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой [ln].

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145 [MR]

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

[MR]

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

Преобразование смешанной дроби в неправильную дробь: онлайн калькулятор

Дробь — это рациональное число, которое представляет собой одну или несколько частей единицы. Наряду с натуральными числами дроби широко используются в бытовых расчетах и реальной жизни.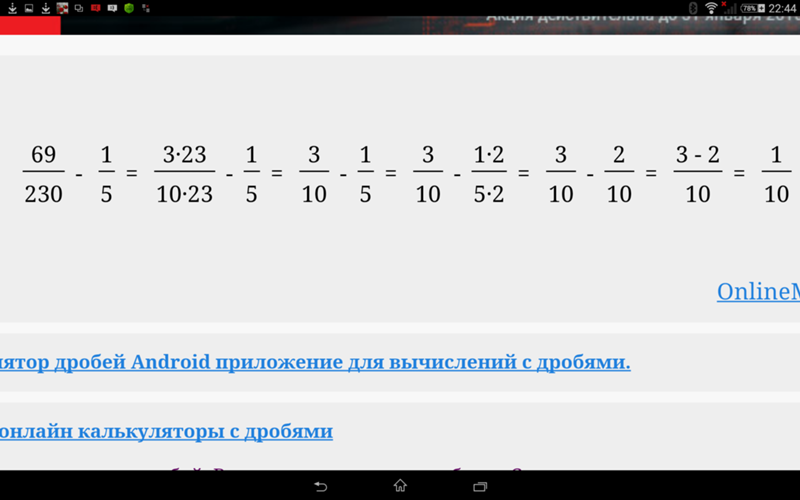

История возникновения

Нужда в дробных числах возникла у людей еще до начала цивилизации. Разделение мяса и шкур убитых животных между участниками охоты иногда приводило к серьезным проблемам, если количество добычи не совпадало с количеством охотников или не было кратным ему. Проблемы с разделением ресурсов привели первобытного человека к понятию дробного числа.

С зарождением цивилизации людям потребовалось вычислять все больше и больше параметров при строительстве жилья и организации сельского хозяйства. Необходимость измерять длины, объемы и площади, которые далеко не всегда можно выразить целым числом, привела к активному использованию дробей в жизни древних людей. Впервые дроби начали использоваться в Древнем Вавилоне и Древнем Египте, причем египтяне применяли дроби исключительно с единицей в числителе. Позднее знание о дробях распространилось по всему миру и появилось на Руси только в VIII веке.

Проблема измерений всегда остро стояла перед человечеством. Если для счета предметов хватает однозначных натуральных чисел, то для измерения параметров их недостаточно. Небольшие ошибки в инженерных расчетах, оперирующих натуральными числами, нередко приводили к разрушению возведенных конструкций. Именно тогда в зодчестве начали активно использовать десятичные дроби для более точного выражения величин. Однако проблема точности вычислений до сих пор актуальна, так как точность можно повышать до бесконечности.

Определение термина

Дробь — это число, состоящее из нескольких долей единицы. Записываются такие числа в виде обыкновенной или десятичной дроби. Обыкновенная дробь имеет общий вид m/n, где n ≠ 0. Рациональные числа имеют две формы записи: через горизонтальную черту, которая называется «винкулум» или через наклонную — «солидус». В нашей статье мы будем использовать солидус для удобства записи.

Если m < n, то такое число является правильной дробью (например, 3/5, 8/10 или 35/100). Если m > n, то такая дробь носит название неправильной (к примеру, 3/2, 8/3 или 54/21). Любое целое число легко записать в форме дроби, и в общем виде это выглядит как m/1. Если же величина записывается в виде комбинации целого числа и правильной дроби, то она носит названия смешанного дробного числа. Такие числа можно преобразовывать из одного вида в другой.

Перевод дробей из одного типа в другой

При решении примеров по арифметике иногда возникает потребность преобразовать неправильную дробь в смешанную или наоборот. Это легко сделать, если использовать следующие алгоритмы. Для преобразования «смешанная — неправильная» нужно:

• целую часть смешанного числа умножить на знаменатель дроби, после чего сложить результат с числителем;
• знаменатель оставить без изменения.

Преобразуем смешанную дробь 4 и 2/3 в неправильную. Умножим целое 4 на знаменатель 3 и результат 12 добавим к числителю. В итоге получаем 14. Знаменатель оставляем без изменений и записываем неправильную дробь 14/3.

Для трансформации «неправильная — смешанная» используется следующий алгоритм:

• числитель делим на знаменатель и полученное число принимаем за целую часть смешанной дроби;
• остаток от деления записываем в числитель обыкновенной дроби, а знаменатель оставляем тем же.

На примере это выглядит так. Для дроби 22/7 разделим 22 на 7, получим 3 и 1 в остатке. После это занесем остаток в числитель правильной дроби и запишем 3 и 1/7.

Если для решения заданий по арифметике требуется перевести целое число в дробь, то в знаменатель просто пишут единицу, а затем приводят дроби к общему знаменателю.

Небольшие дроби легко вручную переводить из одного вида в другой. Однако если требуется выразить в виде неправильной дроби выражение вида 135 и 784/623, то проще воспользоваться нашим онлайн-калькулятором. Инструмент мгновенно переводит смешанные дроби в неправильные и наоборот. Для этого в меню программы следует выбрать направление преобразования и ввести нужное число. Достаточно одного клика мышкой для получения мгновенного результата. Например, при помощи калькулятора легко подсчитать, что 135 и 784/623 тождественно равно неправильной дроби 84889/623.

Заключение

Дробные числа — неотъемлемая часть жизни. Люди пользуются дробями даже в таких простых ситуациях, как разрезание пиццы или подбор пропорций для приготовления коктейля. Умение преобразовывать числа из одной формы в другую несомненно пригодится даже в простых бытовых расчетах, не говоря уже о школьных задачах и профессиональных вычислениях.

Как составить и рассчитать пропорцию: онлайн калькулятор

Онлайн калькулятор пропорций

Формула пропорций

Пропо́рция — это равенство двух отношений, когда a:b=c:d

средние
╭
члены
╮

1
:
10
=
7
:
70
╰
крайние члены
╯

0,1
=
0,1


1
10 = 7
70


 
Основные свойства пропорции
 
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1
10 ✕ 7
70

1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1
10 7
70

10
1 = 70
7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1
10 7
70

1
7 = 10
70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1
10 7
70

70
10 = 7
1

Решение пропорции с одним неизвестным | Уравнение
 
1 : 10 = x : 70



1
10 = x
70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70
10 = 7


Как посчитать пропорцию
 
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию:
1 таблетка — 10 кг
x таблеток — 70 кг

Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение:
1 таблетка
x таблеток ✕ 10 кг
70 кг

x = 1 ⋅ 70 : 10 = 7

Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию:
2 статьи — 5 часов 
x статей — 20 часов

x = 2 ⋅ 20 : 5 = 8

Ответ: 8 статей

Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Деление в столбик с запятыми калькулятор. Обыкновенные и десятичные дроби и действия над ними. Действия с десятичными дробями
Важным элементом государственной территории являются воды, которые делятся на внутренние (водные пути, моря, морские порта, рейды, бухты и т.п., расположенные в пределах государственных границ) и территориальные.
Воды, входящие в состав государственной территории, имеют большое геополитическое значение:
1. Внутренние водные пути (реки, каналы и т.п.) во многих случаях выполняют роль геостратегических линий развития государства: по ним проходят важные транспортные коммуникации; вдоль этих водных путей располагаются города, в том числе и крупные, формируются экономические районы, проживает значительная часть населения страны; внутренние воды играют роль естественных преград при обороне государства;
2. Территориальные воды обеспечивают государству выход к открытому морю и мировой системе морских коммуникаций.
Воздушное пространство имеет важное значение в аспекте транспортных коммуникаций и обороны страны.
Государственные территории всех стран мира вместе с международными проливами, открытым морем и Антарктидой составляют мировое геополитическое пространство.
Геополитическое пространство подразделяется на геостратегические регионы. Геостратегический регион – образуется вокруг государства или группы государств, играющих ключевую роль в мировой политике и представляет собой большое пространство, в которое, помимо территорий регионообразующих стран, входят зоны их контроля и влияния. Геостратегические регионы состоят из геополитических регионов. Геополитический регион – это часть геостратегического региона, отличающаяся более тесными и устойчивыми политическими, экономическими, культурными связями. Геополитический регион более органичен и компактен, чем геостратегический.
Существенную роль в геополитических исследованиях играет категория «граница».
В политическом плане под границей понимают рамки, ограничивающие пространство, на которое распространяется национальный суверенитет. Граница — это не просто линия, механически обозначающая размеживание государственных территорий. Граница является одним из важнейших факторов, обеспечивающих жизнеспособность и безопасность государства. Она определяет ареал формирования национального самосознания и национальной идентичности. Способность государства обеспечивать неприкосновенность и защиту своих границ является показателем его силы и авторитете в международном сообществе. Границы подразделяются на естественные и искусственные. Под естественными границами (моря и океаны, реки и горные цепи) понимают созданные природой рубежи и преграды, которые используются для отделения территории одного государства от другого или от открытого моря. Искусственные границы обустраиваются людьми с помощью специальных инженерных сооружений. В геополитике отдается предпочтение естественным границам над искусственными. Границы выполняют важные геополитические функции. Они разделяют зоны действия национальных суверенитетов, служат рубежами передовой обороны государств, выступают в качестве пунктов контроля за миграцией людей и т. д.
Важным элементом геополитического анализа является сила (или мощь) государства. Категория сила отражает чрезвычайно сложное и многофакторное геополитическое явление. С одной стороны, сила государства – это способность одной державы достигать своих целей во внешней политике путем оказания существенного или определяющего воздействия на политику других стран. С другой стороны, сила связана с возможностями государства отстаивать свои интересы, самостоятельно решать жизненно важные задачи своего политического и экономического развития.
Современная геополитическая теория в наши дни ищет ответ на вопрос, связанный с адекватной оценкой силовых соотношений между государствами современного мира. Эта проблема тесно связана с определением баланса сил в международном сообществе, который является исторической категорией и во многом определяет глобальное развитие всего человечества и отдельных регионов на нашей планете.
Заключение 
Под международной безопасностью нами понимается характеристика международных отношений, включающая в себя такие показатели, как стабильность развития, защищенность от внешних угроз, обеспечение суверенитета и независимости всех государств, признанных мировым сообществом. Основными способами обеспечения международной безопасности являются: двусторонние договоры об обеспечении взаимной безопасности между заинтересованными странами; объединение государств в многосторонние союзы; всемирные между-народные организации, региональные структуры и институты для поддержания международной безопасности; демилитаризация, демократизация и гуманизация международного политического порядка, установление верховенства права в международных отношениях.
В зависимости от масштабов проявления различают следующие уровни международной безопасности: 1) национальный, 2) региональный и 3) глобаль-ный. Такая типология непосредственно связана с важнейшими пространствен-ными категориями геополитической теории, каковыми являются: государственная территория, геостратегические и геополитические регионы; мировое геополитическое пространство.
Государственная территория — это часть земного шара, над которой осу-ществляет суверенитет определенное государство. Сказанное означает, что государственная власть в пределах своей территории обладает верховенством и не зависит от других сил и обстоятельств. Однако такое представление следует отнести к идеальной, существующей в теории модели. На практике государственный суверенитет имеет определенные ограничения, которые накладывают на него взаимодействия страны с другими субъектами международных отношений. Эти ограничения связаны с обязательствами, принимаемыми государствами при заключении международных договоров, в результате вступления в международные организации.
Величина территории, которую занимает то или иное государство на планете, является одним из важнейших показателей, во многом определяющих место страны в иерархии международных отношений, ее политику на мировой арене и национальные геополитические интересы. Размер сухопутной территории при определении геополитического потенциала государства всегда сопрягается с численностью его населения. Сумма государственных территорий всех стран мира вместе с международными проливами, открытым морем и Антарктидой составляет мировое геополитическое пространство. Оно, в свою очередь, подраз-деляется на регионы.
Геостратегический регион образуется вокруг государства или группы государств, играющих ключевую роль в мировой политике, и представляет собой большое пространство, в которое, помимо территорий регионообразующих стран, входят зоны их контроля и влияния. Число подобных регионов обычно крайне ограничено, они занимают громадные пространства и определяют расположение центров силы в мировом сообществе. Эти регионы состоят из геополитических пространств меньшей величины, называемых геополитическими регионами. Геополитический регион — это часть геостратегического региона, отличающаяся более тесными и устойчивыми политическими, экономическими и культурными связями. Геополитический регион более органичен и контактен, чем геостратегический.
Международная безопасность в наше время обеспечивается на различных геополитических уровнях, которые, с одной стороны, образуют единую иерархическую систему всемирного масштаба. С другой стороны, для каждого уровня присущи специфические особенности, собственная конфигурация и механизмы создания условий для достижения приемлемой, гарантированной безопасности. В данной связи, как мы уже отмечали, выделяются три основных вида международной безопасности: национальная, региональная и глобальная.
Идеи, которые в наше время принято причислять к геополитическим, в тех или иных формах, по-видимому, возникли одновременно с феноменом государственной экспансии и имперского государства. В современном понимании они сформировались и получили популярность на рубеже XIX и XX вв. Возникновение именно в тот период геополитических идей и самой геополитики как самостоятельной области исследования международных отношений и мирового сообщества было вызвано целым комплексом факторов: во-первых, наметившиеся к тому времени тенденции к постепенному формированию глобального рынка, уплотнению ойкумены и «закрытию» мирового пространства. Во-вторых, замедление (не в малой степени в силу этого закрытия) европейской, чисто пространственно-территориальной экспансии вследствие завершения фактического передела мира и ужесточение борьбы за передел уже поделенного мира. В-третьих, перенесение в результате этих процессов неустойчивого баланса между европейскими державами на другие континенты «закрывшегося» мира. В-четвертых, образно говоря, история начинала переставать быть историей одной только Европы или Запада, она превращалась уже в действительно всемирную историю. В-пятых, в силу только что названных факторов именно тогда начали разрабатываться теоретические основы силовой политики на международной арене, послужившие в дальнейшем краеугольным камнем политического реализма.
Необходимо учесть и то, что геополитические идеи и сама геополитика возникли и развивались в общем русле эволюции научной мысли того периода. В целом она представляла собой не что иное, как перенесение на сферу международных отношений господствовавших в тот период как в естественных, так и социальных и гуманитарных науках идей и концепций, а именно детерминизма (в его географическом варианте), строгих естественно-исторических законов, социал-дарвинизма и т.д.
Традиционные представления о международных отношениях основывались на трех главных китах — территории, суверенитете, безопасности государств — факторов международной политики. В трактовке же отцов-основателей геополитики центральное место в детерминации международной политики того или иного государства отводилось его географическому положению. В их глазах мощь государства прочно коренится в природе самой земли. Смысл геополитики виделся в выдвижении на передний план пространственного, территориального начала. Поэтому главная задача геополитики усматривалась в изучении государств как пространственно-географических феноменов и постижении природы их взаимодействия друг с другом.
Иначе говоря, традиционная геополитика рассматривала каждое государство как своего рода географический или пространственно-территориальный организм, обладающий особыми физико-географическими, природными, ресурсными, людскими и иными параметрами, собственным неповторимым обликом и руководствующийся исключительно собственными волей и интересами.
Поэтому естественно, что первоначально геополитика понималась всецело в терминах завоевания прямого (военного или политического) контроля над соответствующими территориями.
Список литературы 
1. Баулин Г.К. Геополитическая ситуация в постсоветском пространстве и проблемы военной безопасности России М.: // НЭБ. 1998г. 300с.
2. Казначеев В.П., Дёмин Д. В., Мингазов И. Ф. Геополитика и проблема этногенеза М.: // ТАНДЕМ. 1997г. 402с.
3. Морозов Е.Д. Геополитика в её историческом развитии // Армия. 1998г. №3 35c.
4. Сорокин К.Э. Геополитика и геостратегия России М.: // Инфра-М. 1996г. 340с.
5. Сорокин К.Э. Геополитика мира и России // Политические исследования 1995г. № 1 40с
6. Геополитик: Хрестоматия/Сост. Б.А. Исаев. – СПб.: Питер, 2007. – 512 с.: ил. – (Серия «Хрестоматия»)
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
Цифры.
Знаки арифметических действий.
Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
умножение;
деление;
сложение;
вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
Очень простой, интуитивно понятный интерфейс для каждого пользователя.
Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
 Клавиша
 Обозначение
 Пояснение
 5
 цифры 0-9
 Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
 .
 точка (запятая)
 Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
 +
 знак плюс
 Сложение чисел (целые, десятичные дроби)
 —
 знак минус
 Вычитание чисел (целые, десятичные дроби)
 ÷
 знак деления
 Деление чисел (целые, десятичные дроби)
 х
 знак умножения
 Умножение чисел (целые, десятичные дроби)
 √
 корень
 Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
 x 2
 возведение в квадрат
 Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
 1 / x
 дробь
 Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
 %
 процент
 Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
 (
 открытая скобка
 Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)
 закрытая скобка
 Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
 ±
 плюс минус
 Меняет знак на противоположный
 =
 равно
 Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
 ←
 удаление символа
 Удаляет последний символ
 С
 сброс
 Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.
Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
 сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
 возрастает. Линейное уравнение с десятичными дробями решается точно так же, как и множество других
 уравнений, однако их решение нужно начинать с сокращения уравнения и избавления от десятичных дробей.
Допустим, дано уравнение следующего вида:
Данное уравнение можно решить двумя разными способами.
Способ № 1:
Решение начинаем с упрощения уравнения с помощью открытия скобок, а поскольку перед скобками у нас стоит
 число, то умножаем это число на каждый член в скобках:
Сейчас наше уравнение имеет линейный вид, благодаря чему мы производим перенос неизвестных в одну сторону,
 целый числе в другую:
\[ — 7,2x + 5,2x = 1,7 — 14,4 — 4,3\]
Делим 2 части на число перед \
\[ — 2x = — 17\]
Ответ: \
Способ № 2:
В этом способе умножим левую и правую части на 10:
Это линейное уравнение, которое решается по аналогии с 1 способом:
\[ — 72x + 52x = 17 — 144 — 43\]
\[ — 20x = — 170\]
Ответ: \
Где можно решить десятичные уравнения онлайн?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель
 позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
 просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
 и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
 групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
 рады помочь вам.
Калькулятор дробей  предназначен для быстрого расчета операций с дробями, поможет легко дроби сложить, умножить, поделить или вычесть.
Современные школьники начинают изучение дробей уже в 5 классе, с каждым годом упражнения с ними усложняются. Математические термины и величины, которые мы узнаем в школе, редко могут пригодиться нам во взрослой жизни. Однако дроби, в отличие от логарифмов и степеней, встречаются в повседневности достаточно часто (измерение расстояния, взвешивание товара и т. д.). Наш калькулятор предназначен для быстрого проведения операций с дробями.
Для начала определим, что такое дроби и какие они бывают. Дробями называют отношение одного числа к другому, это число, состоящее из целого количества долей единицы.
Разновидности дробей: 
Обыкновенные
Десятичные
Смешанные
Пример обыкновенных дробей: 
Верхнее значение является числителем, нижнее знаменателем. Черточка показывает нам, что верхнее число делится на нижнее. Вместо подобного формата написания, когда черточка находится горизонтально, можно писать по-другому. Можно ставить наклонную линию, например:
1/2, 3/7, 19/5, 32/8, 10/100, 4/1
Десятичные дроби  являются самой популярной разновидностью дробей. Они состоят из целой части и дробной, отделенные запятой.
Пример десятичных дробей:
0,2, или 6,71 или 0,125
Состоят из целого числа и дробной части. Чтобы узнать значение этой дроби, нужно сложить целое число и дробь.
Пример смешанных дробей:
Калькулятор дробей на нашем сайте способен быстро в онлайн-режиме выполнить любые математические операции с дробями:
Сложение
Вычитание
Умножение
Деление
Для осуществления расчета нужно ввести цифры в поля и выбрать действие. У дробей нужно заполнить числитель и знаменатель, целое число может не писаться (если дробь обыкновенная). Не забудьте нажать на кнопку «равно».
Удобно, что калькулятор сразу предоставляет процесс решения примера с дробями, а не только готовый ответ. Именно благодаря развернутому решению вы можете использовать данный материал при решении школьных задач и для лучшего освоения пройденного материала.
Вам нужно осуществить расчет примера:
После введения показателей в поля формы получаем:
 
Чтобы сделать самостоятельный расчет, введите данные в форму.
Калькулятор комплексных дробей онлайн
Полученный результат в виде дроби

 В отличие от универсального калькулятора Универсальный калькулятор комплексных чисел онлайн, этот калькулятор комплексных  чисел арифметический.

 «Для чего же?» — спросите Вы — «Ведь,  уже есть калькулятор, который считает правильно».

 Отвечаем: Дело в том что хорошо, когда калькулятор считает правильно, но ведь хочеться что бы он считал еще и красиво.

 Представьте — Вы школьник и Вам надо посчитать вот такое выражение


 А еще преподаватель просить выразить результат в виде дроби.

 Вам тогда бы пришлось  проводить деление сразу в виде дроби  потом складывать,  потом  опять преобразовывать в дробь

 Ну да, с помощью универсального калькулятора Вы посчитаете результат выражения, но в красивую дробь он же Вам его не конвертирует.

 А хотелось бы….

 Вот для всех школьников, которые столкнулись с подобными задачами и посвящается этот калькулятор.

 Отличие этого калькулятора в том, что  результат выдает в виде точной дроби, ( если такая будет присутствовать), или приближенной если  в выражении будут присутствовать иррациональные числа.

 Например, очень удобно умножать или делить комплексные числа, которые заданы в виде дроби. 

 Кроме этого, калькулятор переводит число, заданное в виде целой и дробной части, разделенной через точку,  в правильную (или неправильную)  дробь.

 То есть можно назавать эту возможность конвертацией дробей, в том числе и комплексных.

 Синатксис для тех кто пользуется XMPP клиентом

 dr_i выражение

  

 где, выражение — число или выражение в обычной или комплексной форме.

 Примеры


 так и пишем 

  

 dr_i (1+i)/(-2+5i)+(0.2-5.7i)

 Получаем ответ

 Действительная  часть

 Числитель= 44

 Знаменатель= 145

 Мнимая  часть

 Числитель= 1723

 Знаменатель= -290

  
 то есть  ответ  выглядит вот так 

  

 У этого калькулятора есть ограничение:  не всегда при очень малых значения  или при очень больших значениях выдает некорректный результат. Это связано с недостаточной точностью вычислений как языка PHP, так и написанных ботов. Проблема будет решаться постепенно.

  

 Вот пример неудачного вычисления

  

  

 Здесь ответ понятен и правилен 

  

 Но как только мы еще раз разделим исходное выражение, на некотрое число, например на 371

 Ответ будет неверен.

 Но если разделить исходное выражение на 10 000 то ответ опять будет правильным. Эта «плавающая » ошибка требует своего разрешения. На май 2015 года её поймать не удалось.

  

  

 Удачных расчетов!

  
 Калькулятор комплексных дробей онлайн |
2012-12-04 07:40:14 |
Варламов Дмитрий  |  Алгебра  |  Дробный калькулятор комплексных чисел. Конвертер комплексной дроби |
 комплексная, дробь, вычисление, сократить
Калькулятор считает выражения с градусами
Данный калькулятор очень похож на калькулятор, который считает арифметику двоичных чисел:
http://abcname.com.ua/calc/matematika/arithmetic-binary-numbers.html
Только, в данной случае, калькулятор может считать еще и арифметику выражений с градусами.
Калькулятор очень просто работает, но нужно правильно вводить градусы. Даем несколько примером, как правильно прописывать градусы в калькуляторе:
12 — это будет 12 градусов, 0 мин, 0 сек.
12.3 — 12 градусов, 18 мин, 0 сек (доли градуса)
17.4′ — 17 градусов, 4 мин, 0 сек (град/мин)
18.2’6 — 18 градусов, 2 мин, 6 сек (град/мин/сек)
19.4’3′ — 19 градусов, 4 мин, 3 сек (град/мин/сек)
11.8’2» — 11 градусов, 8 мин, 2 сек (град/мин/сек)
14.4.7 — 14 градусов 4 ми, 7 сек (град/мин/сек)
.3 — 0 градусов 18 мин, 0 сек (доли градуса)
и так далее.
 
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1.
Value: ‘%2’.
Error:
%3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
minutes
minutes
minute
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
minutes
hour
hours
hours
hours
hours
hours
hours
hours
hours
hours
hours
days
day
day
day
day
days
days
days
days
days
days
days
month
month
month
month
months
months
months
months
months
months
months
year
of the year
of the year
of the year
years
years
years
years
years
years
years
ago
%1 minutes ago
%1 minutes ago
%1 minutesу ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 minutes ago
%1 hour ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 hours ago
%1 days ago
%1 day ago
%1 day ago
%1 day ago
%1 day ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 days ago
%1 month ago
%1 month ago
%1 month ago
%1 month ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 months ago
%1 year ago
%1 of the year ago
%1 of the year ago
%1 of the year ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
%1 years ago
 Калькулятор действий над градусами
 Результат вычисления (градусы/minutes/секунды):
 Результат вычисления (доли градуса):
 Калькулятор среднего значения
 | Калькулятор среднего вниз
 
 Онлайн-калькуляторы> Финансовые калькуляторы> Калькулятор средней стоимости акций
  Калькулятор средней стоимости запасов  рассчитывает среднюю стоимость ваших акций, когда вы покупаете одни и те же акции несколько раз.  Калькулятор среднего вниз  даст вам среднюю стоимость за среднее снижение или среднее повышение. Если вы покупаете одни и те же акции несколько раз, вводите каждую транзакцию отдельно.Приведенная ниже формула средней акции показывает, как рассчитать среднюю цену.
 Ниже показаны результаты калькулятора среднего значения  акций .
 Всего акций
 Средняя стоимость
 Калькулятор расчета средней стоимости
 Если у вас есть устройство Android, вы можете узнать среднюю стоимость ваших покупок на складе с помощью калькулятора  средней стоимости , который вы можете установить бесплатно.Получите калькулятор средней стоимости акций для Play Store. 
 Ниже приведена формула  средней пуховой акции , которая показывает, как рассчитать среднюю цену.
 Формула среднего запаса
 Ниже приводится формула средней стоимости акций для расчета средней цены акции, если вы купили одну и ту же акцию n раз. 
 1. Общее количество купленных акций = купленных акций (1-е) + купленных акций (2-е) + купленных акций (3-е) + …. купленных акций (n-е) 
 2. Общая сумма купленных акций = купленные акции * покупная цена (первая) + купленные акции * покупная цена (вторая) + купленные акции * покупная цена (третья) +…. Купленных акций * Цена покупки (л.) 
 3. Средняя цена акций = Общая сумма купленных / Всего купленных акций
 Если вы хотите рассчитать прибыль от акций,
воспользуйтесь простым калькулятором запасов.
 Как торговать акциями
 Чтобы узнать, как торговать акциями с целью получения прибыли, вы можете прочитать следующие три книги о том, как торговать акциями и инвестировать в них. 
 1. Как заработать на акциях 
 
 2. Интеллектуальный инвестор 
 
 3.Как вести дневную торговлю, чтобы заработать на жизнь 
 
 Калькулятор прибыли от акций 
 Калькулятор дивидендов 
 Калькулятор модели скидки на дивиденды 
 Калькулятор Фибоначчи 
 Калькулятор EPS 
 Калькулятор коэффициента P / E 
 Калькулятор цены акций для оценки обыкновенных акций
 Какая требуется норма доходности
 Формула оценки обыкновенных акций, используемая при этом Калькулятор оценки акций основан на модели роста дивидендов  , которая является лишь одной из нескольких моделей оценки акций, используемых инвесторами для определения того, сколько они должны быть готовы платить за различные акции.
 Модель роста дивидендов для оценки обыкновенных акций предполагает, что дивиденды  будут выплачены , а также предполагает, что дивиденды будут расти постоянными темпами в течение неопределенного периода времени. Конечно, ни одно из этих предположений редко, если вообще случается, в реальной жизни.
 Как рассчитать стоимость акций
 Чтобы определить стоимость обыкновенных акций с использованием модели роста дивидендов, вы сначала определяете будущий дивиденд, умножая текущий дивиденд на десятичный эквивалент процента роста (дивиденд x (1 + рост ставка)).
 Наконец, будущий дивиденд делится на разницу между десятичным эквивалентом ожидаемой нормы прибыли и десятичным эквивалентом процента роста (будущие дивиденды ÷ (ожидаемая норма прибыли — темп роста)).
 Чтобы проиллюстрировать, как рассчитать стоимость акций с использованием формулы модели роста дивидендов, если текущая цена дивидендов по акции составляла 0,56 доллара США, а темпы роста — 1,300%, а требуемая норма доходности составляла 7,200%, следующий расчет показывает наибольшую Вы бы хотели заплатить за эту акцию 9 долларов.61 за акцию.
 Расчет стоимости акций с использованием модели роста дивидендов
 Переменная
 Формула
 Результат
 Будущий дивиденд =
 Дивиденд x (1 + (темп роста / 100))
 Будущее дивиденд =
 0,56 x (1 + (1,3 / 100))
 Будущий дивиденд =
 0,56 x (1 + (0,013))
 Будущий дивиденд =
 0.56 x 1,013 =
 0,57
 Разница ставок =
 Требуемая скорость — Скорость роста
 Разница ставок =
 0,072 — 0,013 =
 0,059
 Цена акции =
 Будущие дивиденды / Разница в ставках
 Цена акции =
 0,57 / 0,059 =
 9,61 долл. США
 Что такое требуемая норма прибыли?
 В отличие от облигаций, где риск потери основной суммы минимален, а дивиденды выплачиваются в виде фиксированного процента, акции связаны с повышенным риском потери основной суммы, а дивиденды по акциям никогда не гарантированы, а дивиденды на акцию не являются фиксированными.
 Эти дополнительные риски и неопределенности при инвестировании в акции объясняют, почему инвесторы рассчитывают получить более высокую отдачу от инвестиций в акции, чем в облигации. Другими словами, больший риск означает более высокую ожидаемую доходность.
 Это различие между ожидаемой нормой доходности с низким уровнем риска (например, ставкой казначейских векселей) и более высокой ожидаемой нормой доходности, обусловленной повышенным риском, часто называется премией за риск  .
 Премию за риск можно представить как процент, который необходимо добавить к безрисковой прибыли на инвестиции, чтобы побудить инвестора вложить средства в предлагаемые рискованные инвестиции.После добавления этого процента результат будет обозначаться как требуемая норма прибыли  .
 Определите вашу прибыль от позиции по акциям
 Когда люди ищут калькулятор прибыли от акций, они обычно стремятся быстро определить совокупную доходность инвестиций. Это просто говорит вам о вашей общей прибыли от инвестиций независимо от периода времени, в течение которого вы держали эти инвестиции.
 Годовая доходность также полезна тем, что вы можете немного легче сравнивать инвестиции.Например, если вы сравните совокупный доход от инвестиций, которые вы держали в течение двух дней, с инвестициями, которые вы держали в течение 20 лет, это не даст вам ничего слишком проницательного. Сравнение годовой прибыли помогает немного нормализовать результаты и обеспечивает более значимое сравнение.
 Более того, при использовании калькулятора прибыли по акциям мы захотим учесть все элементы доходности, чтобы получить расчет общей доходности. (365 / дни) — 1) x 100%
 А как насчет нескольких акций?
 Что делать, если у вас есть несколько акций и вы хотите определить свою общую прибыль? Что ж, если вы просто хотите просуммировать затраты, выручку и прибыль, вы можете определить совокупный доход, используя формулу выше.Если периоды удержания одинаковы для всех позиций по акциям, вы также можете получить годовую доходность. В большинстве случаев периоды удержания всех ваших позиций не будут в точности одинаковыми, поэтому годовая доходность в этом типе сценария использования имеет некоторые проблемы.
 Если вы пытаетесь определить прибыль портфеля, вам также необходимо учитывать размер позиции. Кроме того, доходность портфеля обычно предполагает, что позиции просто удерживаются (а не покупаются и продаются). Если вы хотите рассчитать доходность портфеля акций и знаете доходность отдельных позиций, вы можете использовать эту формулу:
 Доходность портфеля = (Размер позиции 1 x доходность 1) +….+ (Размер позиции n x возврат позиции n)
 Давайте покажем краткий пример, чтобы убедиться, что вы понимаете концепцию. Допустим, у вас есть три позиции:
 Позиция 1: 25000 долларов с доходностью 10%
 Позиция 2: 25000 долларов с доходностью 15%
 Позиция 3: 50 000 долларов с доходностью 5%
 Теперь вы можете использовать нашу формулу доходности портфеля, чтобы определить общую доходность портфеля как следует:
 Доходность портфеля = (.25 * 10%) + (0,25 * 15%) + (0,5 * 5%)
 Доходность портфеля = (0,25 * 0,1) + (0,25 * 0,15) + (0,5 * 0,05)
 Доходность портфеля = 0,025 + 0,0375 + 0,025
 Доходность портфеля = 0,0875
 Доходность портфеля = 8,75%
 Превзойдите рынок с Titan
 Titan — хедж-фонд мирового класса в вашем кармане. Получите доступ с минимальными инвестициями в 100 долларов к портфелю тщательно отобранных акций исследовательской группы Titan. Если вы хотите что-то более активное, чем пассивное инвестирование в индексные фонды, попробуйте Titan.
 Зарегистрируйтесь сейчас
 или прочтите наш полный обзор для получения дополнительной информации
 Создайте свой собственный калькулятор прибыли от акций с помощью Google Таблиц
 Мне нравится использовать Google Таблицы для различных инструментов отслеживания инвестиций, и создать калькулятор прибыли от акций в Google Таблицах очень просто. Более того, с функциями котировок в реальном времени, которые поставляются с Google Таблицами, вы можете построить свой калькулятор прибыли для оперативного обновления данных на лету. Давайте посмотрим, как мы можем это построить.
 Сначала мы создадим простую версию этого, а затем создадим модифицированную версию, используя данные о реальных запасах.
 Простой калькулятор прибыли от акций с использованием Google Таблиц
 Для нашей начальной версии давайте просто создадим несколько простых полей ввода для следующего: количество акций, цена покупки, цена продажи, выплаченные комиссионные, полученные дивиденды. Затем мы создадим простые формулы для суммирования затрат и выручки и, конечно же, формулу для получения прибыли от затрат и выручки. Это будет выглядеть примерно так:
 Затем мы можем добавить кумулятивный доход, чтобы завершить простой калькулятор прибыли от акций.
 Хорошо, давайте немного поработаем над нашей следующей версией.
 Более продвинутый калькулятор прибыли от акций с использованием Google Таблиц
 В этой более продвинутой версии давайте добавим данные о живом поголовье, а также рассчитаем период владения, который даст нам годовой доход в дополнение к совокупному доходу.
 Мы собираемся немного изменить настройку, чтобы удалить цену продажи и просто обновить ее, указав текущую цену. Это означает, что мы в основном вычисляем прибыль по позиции на лету и предполагаем, что еще не продали ее. Чтобы немного упростить примеры, давайте также уберем комиссии. Вот наша начальная настройка:
 Какие заметные отличия? Сначала я добавил строку для биржевого тикера. В моем примере я использовал Apple (AAPL). Я вручную установил закупочную цену в 250 долларов и вручную установил полученные дивиденды в размере 75 долларов. Затем в ячейке B5 я использовал функцию GOOGLEFINANCE, чтобы получить текущую цену акций Apple. Затраты, выручка, прибыль и совокупный доход рассчитываются на основе этой информации, как и в нашем более простом примере, который мы только что сделали. Примечание. Подробнее об использовании функции GOOGLEFINANCE в Google Таблицах можно узнать здесь .
 Теперь мы хотим добавить дату покупки, добавить ячейку, которая автоматически извлекает текущую дату, а затем добавить формулу внизу для годовой прибыли. Давайте посмотрим:
 Я вручную ввел дату покупки в B4. Затем я использовал функцию Google = СЕГОДНЯ () для ячейки B7, чтобы дата обновлялась каждый день вместе с текущей ценой акций. Затем я вычел две даты в ячейке B19, чтобы получить количество проведенных дней.
 Итак, у меня есть вся необходимая информация для реализации формулы годовой прибыли на основе формулы, приведенной ранее в этой статье.
 Теперь вы можете использовать полученную информацию и при необходимости расширять свою электронную таблицу. Вы можете добавить расчеты для нескольких акций или даже начать расчет прибыльности всего портфеля. Таблицы Google действительно являются отличным ресурсом для создания различных инструментов отслеживания для инвесторов.
 Калькулятор маржи
 Калькулятор прибыли
 Рассчитайте маржу прибыли от производства, торговли продуктами или ведения бизнеса в целом. Для расчета третьего значения укажите любые два из следующих значений.
 Результат
  Валовая маржа: 
  50,00% 
 Валовая прибыль:
 100,00 долларов США
 Наценка:
 100. 00%
  Стоимость:  Стоимость товара.
  Наценка:  Процент прибыли по сравнению с Стоимость.
  Доход от продажи:  Доход от продажи продукта.
  Валовая прибыль:  Процент валовой прибыли продукта по сравнению с доход.
  Валовая прибыль:  Валовая прибыль продукта в денежной сумме.

 Калькулятор маржи для торговли акциями
 Рассчитайте необходимую сумму или поддерживающую маржу, необходимую инвесторам для покупки ценных бумаг с маржой.
 Результат
 Требуемая сумма:  $ 549,00 
  Цена акции:  Цена акции.
  Количество акций:  Количество акций, которые вы хотите приобрести.
  Требование к марже:  Процент, необходимый брокеру для совершения маржинальной покупки.
  Требуемая сумма:  Минимальная сумма, необходимая на вашем счете для покупки.

 Калькулятор маржи обмена валюты
 Рассчитайте минимальную сумму, которую необходимо поддерживать на маржинальном счете для торговли валютой.
 Результат
 Требуемая сумма:  6.500 
  Обменный курс:  Обменный курс валюты для покупки в вашей домашней валюте. Например, если вы планируете купить 100 евро, а ваша домашняя валюта — доллары США. На валютном рынке 1 евро = 1.22 USD, то курс обмена: 1.22.
  Коэффициент маржи:  Отношение маржи к использованию.
  Единиц:  Сумма валюты для покупки.
  Требуемая сумма:  Сумма, необходимая в вашей национальной валюте для совершения покупки.
 Слово «маржа» имеет много разных определений в разных контекстах, таких как ссылка на край или границу чего-либо, или на величину, на которую элемент отстает или превосходит другой элемент.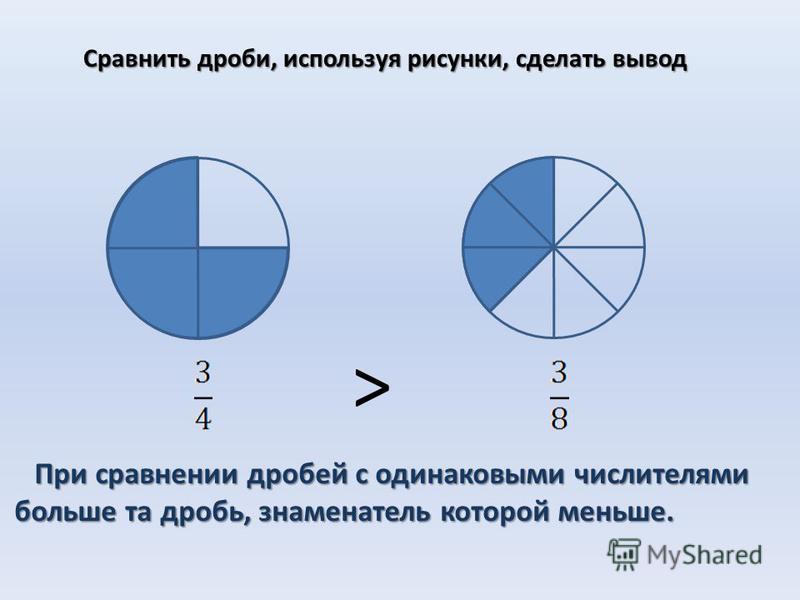 С финансовой точки зрения маржа может относиться к нескольким конкретным вещам. Во-первых, это может быть разница между продажной ценой продукта или услуги и стоимостью его производства (что используется при первом расчете) или это может быть соотношение между доходами и расходами компании. Он также может относиться к сумме собственного капитала, внесенной инвестором, в виде процента от текущей рыночной стоимости ценных бумаг, хранящихся на маржинальном счете (в отношении второго и третьего расчета), или части процентной ставки по регулируемой ставке. ипотека добавлена ​​к ставке индекса корректировки.
 Маржа прибыли
 Маржа прибыли — это сумма, на которую выручка от продаж превышает затраты в бизнесе, обычно выражается в процентах. Его также можно рассчитать как чистую прибыль, деленную на выручку, или чистую прибыль, деленную на продажи. Например, 30% прибыли означает, что на каждые 100 долларов дохода приходится 30 долларов чистой прибыли. Как правило, чем выше маржа прибыли, тем лучше и единственный способ ее улучшить — это снизить затраты и / или увеличить выручку от продаж. Для многих предприятий это означает либо повышение цены на продукты или услуги, либо снижение стоимости продаваемых товаров.
 Маржа прибыли может быть полезна по-разному. Во-первых, его обычно используют как способ оценить финансовое состояние бизнеса. Например, год, который не соответствует типичной норме прибыли в прошлые годы, может указывать на что-то неправильное, например, неправильное управление расходами по отношению к чистым продажам. Во-вторых, маржа прибыли — это показатель эффективности, поскольку она помогает ответить на вопрос: сколько прибыли получается на каждый доллар, полученный в качестве дохода?
 Маржа прибыли также может быть сравнена с показателями компаний-конкурентов, чтобы определить относительную эффективность, прозрачную в соответствии с отраслевыми стандартами.Важно, чтобы сравниваемые компании были довольно похожи по размеру и отрасли.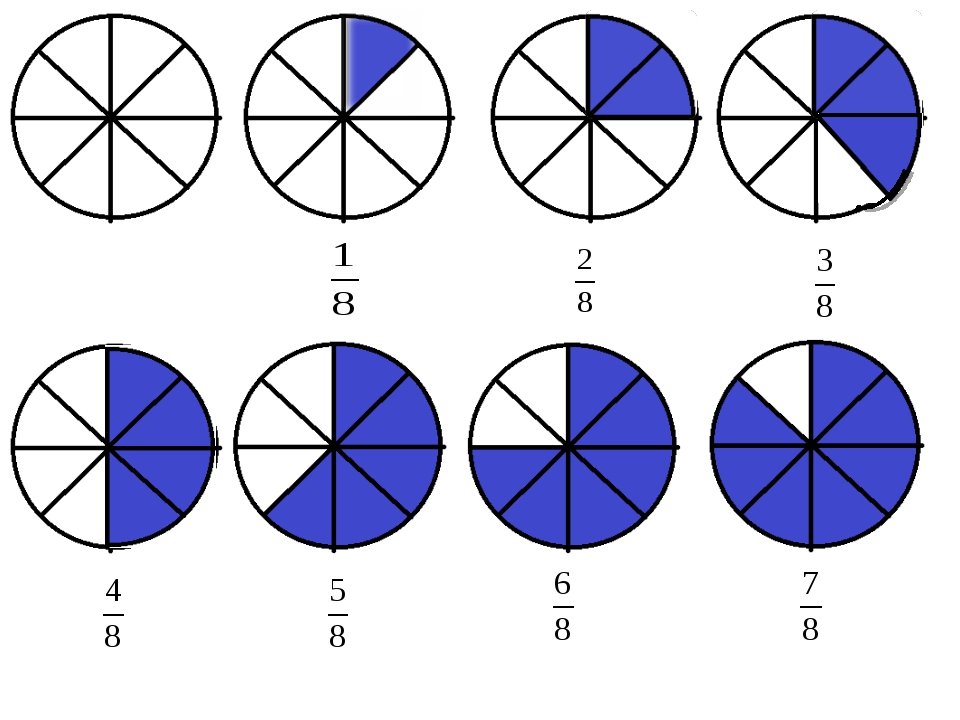 Например, сравнение рентабельности небольшого семейного ресторана с рентабельностью химической компании из списка Fortune 500 не даст особо значимых результатов из-за различий в отрасли и масштабах.
 Маржинальная торговля
 Маржинальная торговля — это практика использования заемных средств у брокеров для торговли финансовыми активами; По сути, это означает вложение заемными деньгами.Обычно речь идет о залоге, таком как акции или другие ценные финансовые активы.
 Покупка акций с использованием заемных денег известна как «маржинальная торговля». Маржинальная торговля имеет тенденцию увеличивать прибыль и / или убытки; например, когда цена активов на счете растет, маржинальная торговля позволяет инвесторам использовать кредитное плечо для увеличения своей прибыли. Однако, когда цены на эти активы падают, потеря стоимости намного больше, чем при обычной торговле активами. Несмотря на это, федеральные правила разрешают заемщикам-инвесторам брать взаймы до 50% от общей стоимости любой покупки в качестве начального маржинального требования.Впоследствии Регламент T Федеральной резервной системы требует поддержания маржи не менее 25%, хотя брокерские фирмы обычно требуют больше. Имейте в виду, что начальные маржинальные требования отличаются от требований поддерживающей маржи.
 Эта форма маржинального инвестирования очень рискованна, и инвесторы (заемщики) должны сначала ознакомиться с рисками.
 Валютная маржа
 В контексте обмена валюты маржу можно рассматривать как добросовестный депозит, необходимый для поддержания открытых позиций, аналогичный залогу, необходимому для аренды.Однако это не комиссия, а часть средств на счете, которая распределяется в качестве маржинального депозита.
 Маржинальное требование — это кредитное плечо, предлагаемое брокером, которое обычно обновляется не реже одного раза в месяц с учетом волатильности рынка или обменных курсов валют. Требование маржи в 2% эквивалентно предложению кредитного плеча 50: 1, которое позволяет инвестору торговать на рынке с 10000 долларов США, откладывая только 200 долларов в качестве гарантийного депозита.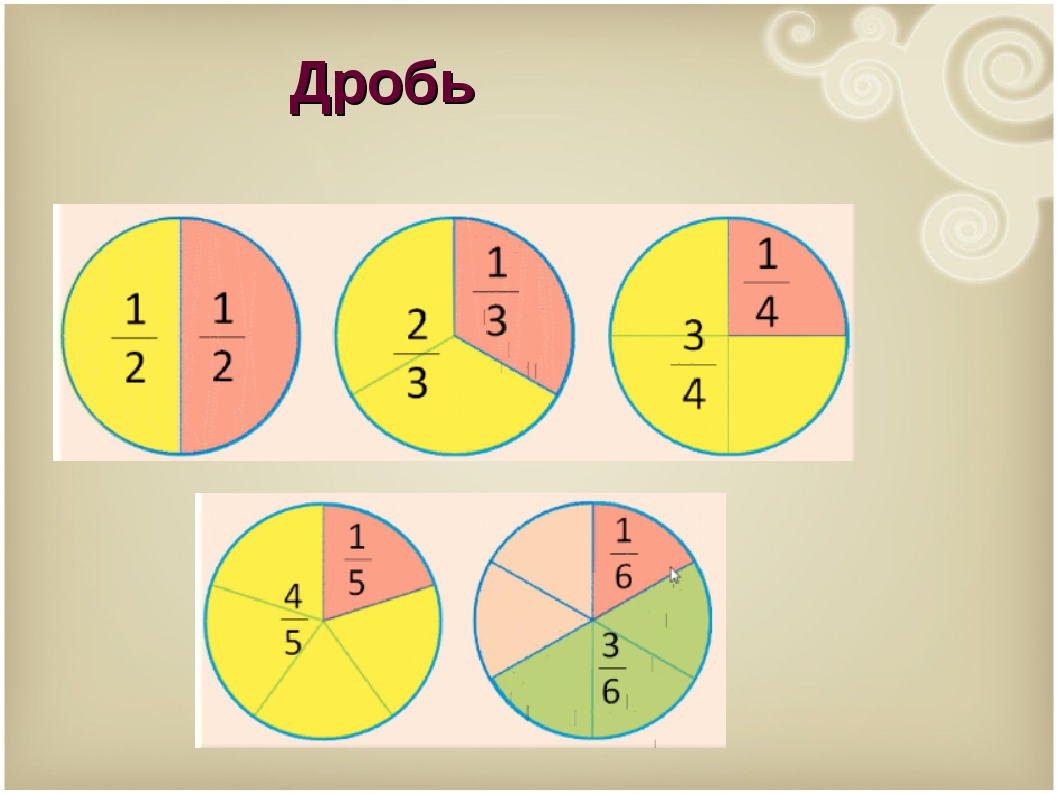 В качестве другого примера маржинальное требование в 1% называется кредитным плечом 100: 1 и позволяет торговать на рынке на сумму 10 000 долларов с залогом в размере 100 долларов.На валютном рынке трейдеры, как правило, торгуют с кредитным плечом 50: 1, 100: 1 или 200: 1 в зависимости от брокера и правил.
  Маржинальное требование 
 Если рынок движется против трейдера, что приводит к таким убыткам, что маржа недостаточна, применяется автоматический маржинальный запрос. Обычно это происходит потому, что на счете больше нет денег, чтобы выдержать потерю стоимости акций, и брокер начинает нести ответственность за убытки.В этом сценарии, если владелец учетной записи не вносит средства для восстановления учетной записи до минимального необходимого уровня обслуживания, брокер закрывает все позиции владельца учетной записи на рынке и устанавливает лимиты на убытки для владельца учетной записи, чтобы остановить учетную запись. от превращения в отрицательный баланс.
 Калькулятор длинного сложения
 Использование калькулятора
 Сложите целые и десятичные числа, используя длинное сложение, показывающее работу.В этом калькуляторе показаны все этапы сложения чисел длинным сложением.
  Разделяйте значения запятыми или новой строкой . Например, при добавлении используйте любой из следующих форматов:
 123,456,7890
 123 
 456 
 7890
 0.987,65,4,32,1
 0,987 
 65,4 
 32,1
 Не используйте запятую в качестве разделителя тысяч. Вводите только положительные числа.
 Сложение целых чисел длинным сложением
 Длинное сложение — это процесс сложения чисел.
 Сложите числа и выровняйте столбцы по разрядам.
 Сложите все числа столбец за столбцом справа налево.
 Запишите сумму в поле для ответов для каждого столбца.
 Если сумма любого столбца больше девяти, перенесите дополнительные цифры в следующий столбец с наибольшим значением.
 Пример: сложение длинным сложением 937 + 129 + 248
  Длинные шаги добавления:  
 Сложите и выровняйте числа по столбцам разряда
  Единицы  Значение места 
 7 + 9 + 8 = 24 
 Поместите 4 на место 
 Отнести 2 к десяткам 
 
  Десятки  Разрядная стоимость 
 2 + 3 + 2 + 4 = 11 
 Поставьте 1 в разряде десятков 
 Отнести 1 к сотням 
 
 
  Сот  Значение места 
 1 + 9 + 1 + 2 = 13 
 Поставьте тройку на место сотен 
 Отнесите 1 к тысяче мест 
 
 
  Тысяч  Значение места 
 1 = 1 
 Поставьте 1 в разряде тысяч 
 Сложение десятичных чисел с длинным сложением
 Процесс длинного сложения с десятичными знаками такой же, как и процесс длинного сложения целых чисел с добавленным столбцом для десятичных знаков. Точно так же, как значения разряда располагаются в одном столбце, все десятичные точки располагаются в одном столбце. Если ваши отдельные числа имеют разное количество десятичных разрядов, вы можете дополнить правую часть нулями, пока все они не будут иметь одинаковое количество десятичных знаков.
 Например, добавьте 37,5 + 129,44 + 48,123
 Связанные калькуляторы
 Посмотреть
 Длинное вычитание с калькулятором перегруппировки, чтобы выполнить долгое вычитание с перегруппировкой или заимствованием и увидеть результат.
 Калькулятор сумматора
 Использование калькулятора
 Этот калькулятор счетной машины полезен для хранения промежуточной суммы или «бумажной ленты» при добавлении или вычитании денег, например, при балансировании вашей чековой книжки, уплате налогов или любых других расчетах, когда вам нужно дважды проверить свои записи. Введите значения и операторы в калькулятор и просмотрите приведенные выше математические расчеты.Распечатайте «ленту» арифметической машины, чтобы сохранить запись ваших вычислений.
  Ограничение памяти составляет 100 записей , но вы можете нажать кнопку «Сброс», чтобы очистить все записи и начать заново.
 Работа и настройки сумматора
   auto   Режим позволяет вам использовать эту суммирующую машину только с вашей клавиатурой, используя числа, десятичные дроби, операторы и клавишу Enter.
   автоматический десятичный режим   режим такой же, как автоматический режим, но предполагает, что ваша запись имеет 2 десятичных разряда. Например, если вы введете 5236 в  автоматический десятичный режим  и нажмите клавишу Enter, калькулятор вставит десятичную точку перед двумя последними цифрами, так что ваша запись станет 52,36. Если вы хотите ввести ровно 52 в  автоматический десятичный режим  необходимо ввести 5200.
 Для  авто  и  автоматические десятичные режимы , функция по умолчанию — сложение (+). Если вы введете только числа и нажмете Enter, калькулятор сложит числа. Вы можете использовать клавиатуру для ввода любого оператора перед вводом номера. Используйте клавиши + — * и / для сложения, вычитания, умножения и деления соответственно.
 Вы также можете вводить числа со знаком% в конце, чтобы операнд составлял процент от текущей суммы.Например, если текущая сумма составляет 300, и вы вводите + 20%, калькулятор найдет 20% от 300 (что составляет 60) и добавит это число к общей сумме. Новое количество — 360.
  автоматический режим  примеры 
  (по умолчанию + )
 25  25  25 
 25 + 25 + 25 = 75
 -25  -25  +25 
 -25-25 + 25 = -25
 25  * 25  / 5 
 25 * 25 = 625 
 625/5 = 125
 25  * 25  / 5  + 20%
 25 * 25 = 625 
 625/5 = 125 
 125+ (20% из 125) 
 125 + 25 = 150
 Расчет налога с продаж
 Рассчитайте 6.
 Налог 25% от вашей суммы, введя + 6,25% в последнюю очередь.
 В этом примере расчета с помощью онлайн-калькулятора счетной машины рассчитывается налог с продаж для детализированной покупки.
 Предположим, вы продали три товара по цене 26,95, 14,75 и 9,99 и должны собрать налог с продаж в размере 6,25% вместе с общей покупкой. Введите следующее (+26.95  +14.75  +9.99  6.25% ). Ваша лента калькулятора покажет промежуточный итог 51.69, налог в размере 6,25% в размере 3,23 и в сумме 54,92, как на изображении ниже.
 Для получения дополнительной помощи по балансировке вашей чековой книжки см.
 Калькулятор баланса чековой книжки.
 Калькулятор прибыли
 — Investing.com
 © 2007-2021 Fusion Media Limited. Все права защищены
 Раскрытие рисков: Торговля финансовыми инструментами и / или криптовалютами сопряжена с высокими рисками, включая риск потери части или всей суммы ваших инвестиций, и может не подходить для всех инвесторов.Цены на криптовалюты чрезвычайно изменчивы и могут зависеть от внешних факторов, таких как финансовые, нормативные или политические события. Маржинальная торговля увеличивает финансовые риски. 
 Прежде чем принять решение о торговле финансовыми инструментами или криптовалютами, вы должны быть полностью проинформированы о рисках и затратах, связанных с торговлей на финансовых рынках, тщательно обдумать свои инвестиционные цели, уровень опыта и склонность к риску и при необходимости обратиться за профессиональной консультацией. 
  Fusion Media  напоминает вам, что данные, содержащиеся на этом веб-сайте, не обязательно являются точными и актуальными в реальном времени.Данные и цены на веб-сайте не обязательно предоставляются каким-либо рынком или биржей, но могут предоставляться маркет-мейкерами, поэтому цены могут быть неточными и могут отличаться от фактических цен на любом данном рынке, то есть цены являются ориентировочными, а не подходит для торговых целей.