Задания в старшей группе по математике: Программные задачи по математике для старшей группы (5-6 л.)

Конспект занятия по математике в старшей группе «Занимательная математика»

Муниципальное дошкольное образовательное учреждение

детский сад общеразвивающего вида №19 «Яблонька»

Конспект занятия по математике в старшей группе

«Занимательная математика»

Подготовила воспитатель: Короткова Т. В.

с. Барановское

Московская область

Цель: создание условий для закрепления математических знаний.

Задачи:

• обобщить знания детей о целом и частях, закрепить умение делить предмет на две, четыре части;

• уточнить знания о прямом и обратном счете;

• уточнить знания о геометрических фигурах;

• продолжить формировать умение находить значение выражений;

• стимулировать развитие мыслительных способностей, любознательность, познавательность;

• продолжить формировать умение четко, быстро отвечать на поставленные вопросы;

• воспитывать дружеские взаимоотношения между детьми, стремление радовать старших своими достижениями, воспитывать интерес к занятиям математики.

Ход занятия

Организационный момент

Воспитатель

Дети заходят, здороваются с гостями.

Для начала встанем в круг,

Сколько радости вокруг!

Мы все за руки возьмемся

И друг другу улыбнемся.

Мы готовы поиграть,

Молодцы! А сейчас внимательно послушайте меня. 

Сегодня у нас необычное занятие. Я приготовила для вас сюрприз, но вы сможете его найти, если пройдете все испытания. На каждом испытании вам будет дана подсказка. Задания будут сложными, но интересными. Выполнив все задания, вы узнаете, какой сюрприз нас ждет. 
Вы готовы? Тогда удачи!

Воспитатель : Какое сейчас время года?

Дети : Зима

Воспитатель: Перечислите все зимние месяцы.

Дети : Декабрь, Январь, Февраль

Воспитатель: Сейчас утро, день или вечер?

Дети: Утро

Воспитатель: Назовите по порядку дни недели.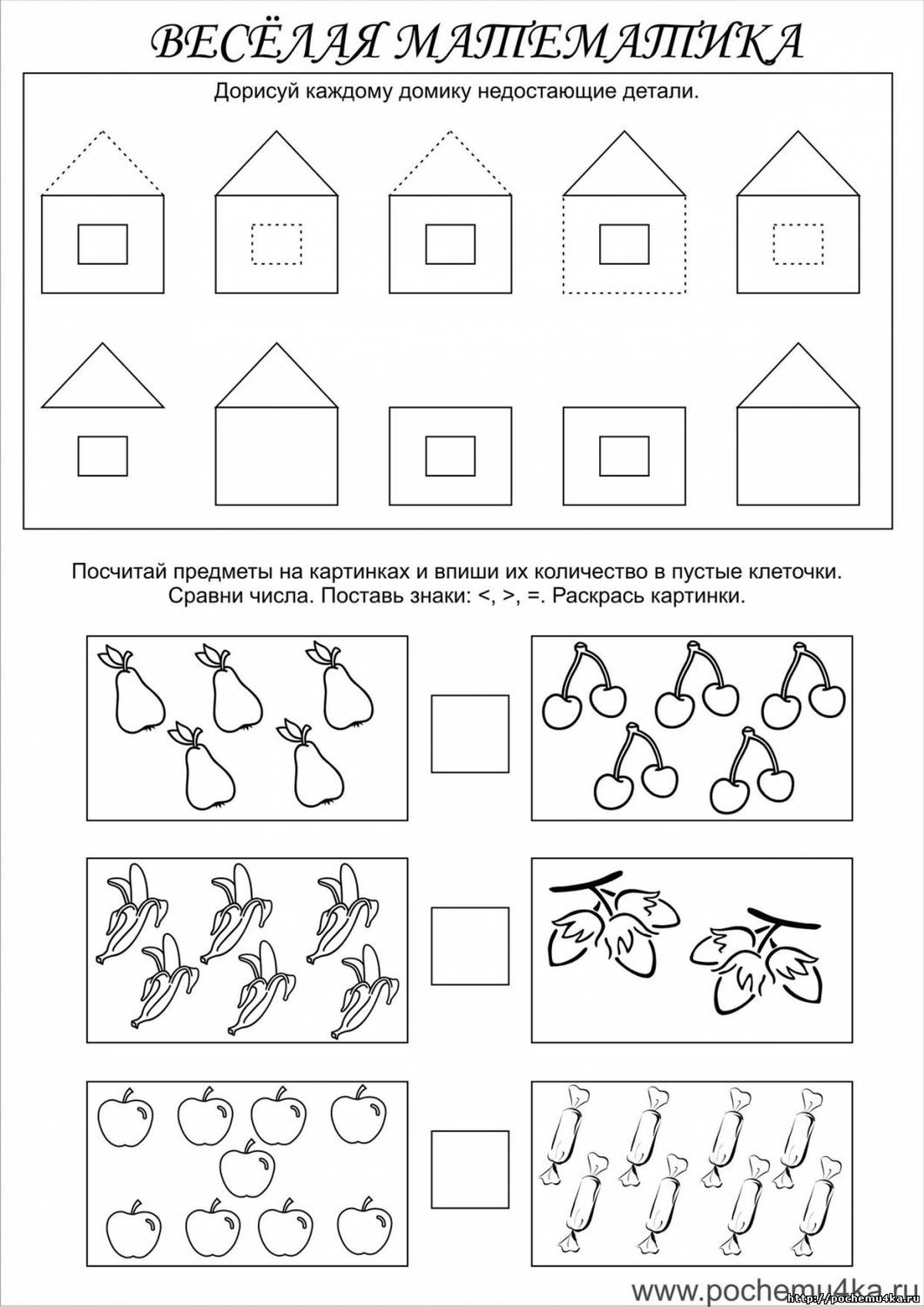

— Сколько пальцев на правой руке? (5)

 — Сколько глаз у светофора?(3)

 — Сколько носов у двух собак?(2)

 — Сколько ушей у двух мышей?(4)

 — Сколько хвостов у двух котов?(2)

— Сколько спинок у трех свинок? (3) 

— Сколько животиков у пяти бегемотиков? (5) 

— Сколько домишек у ста муравьишек? (1) 

Физминутка

В понедельник я купался, Изображаем плавание.

А во вторник –рисовал. Изображаем рисование.

В среду долго умывался, Умываемся.

А в четверг в футбол играл. Бег на месте.

В пятницу я прыгал, бегал, Прыгаем. Кружимся на месте.

Очень долго танцевал. Хлопки в ладоши.

А в субботу, воскресенье Дети садятся на корточки, руки

Целый день я отдыхал. под щеку — засыпают.

Воспитатель: Молодцы, вы очень внимательны, правильно ответили на все вопросы.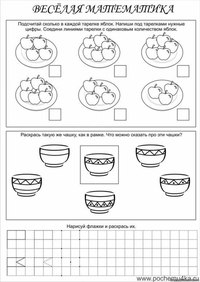 И я вам даю подсказку. Прикрепляю на доску первую подсказку

Воспитатель: Ребята, что это?

Дети: Прямоугольник

Дети: грустное, невеселое

Воспитатель: А почему он загрустил?

Дети: потому, что он один, рядом нет его друзей

Воспитатель: А с кем у нас дружит прямоугольник?

Дети: с кругом, квадратам, овалом, треугольником

Игра «Загадки — отгадки».

Три вершины,

Три угла,

Три сторонки –

Кто же я? Треугольник.

Нет углов у меня

И похож на блюдце я,

На тарелку и на крышку,

На кольцо, на колесо.

Кто же я такой, друзья?

Назовите вы меня! Круг.

Он похожий на яйцо

Или на твое лицо.

Вот такая есть окружность —

Очень странная наружность:

Круг приплюснутым стал.

Получился вдруг….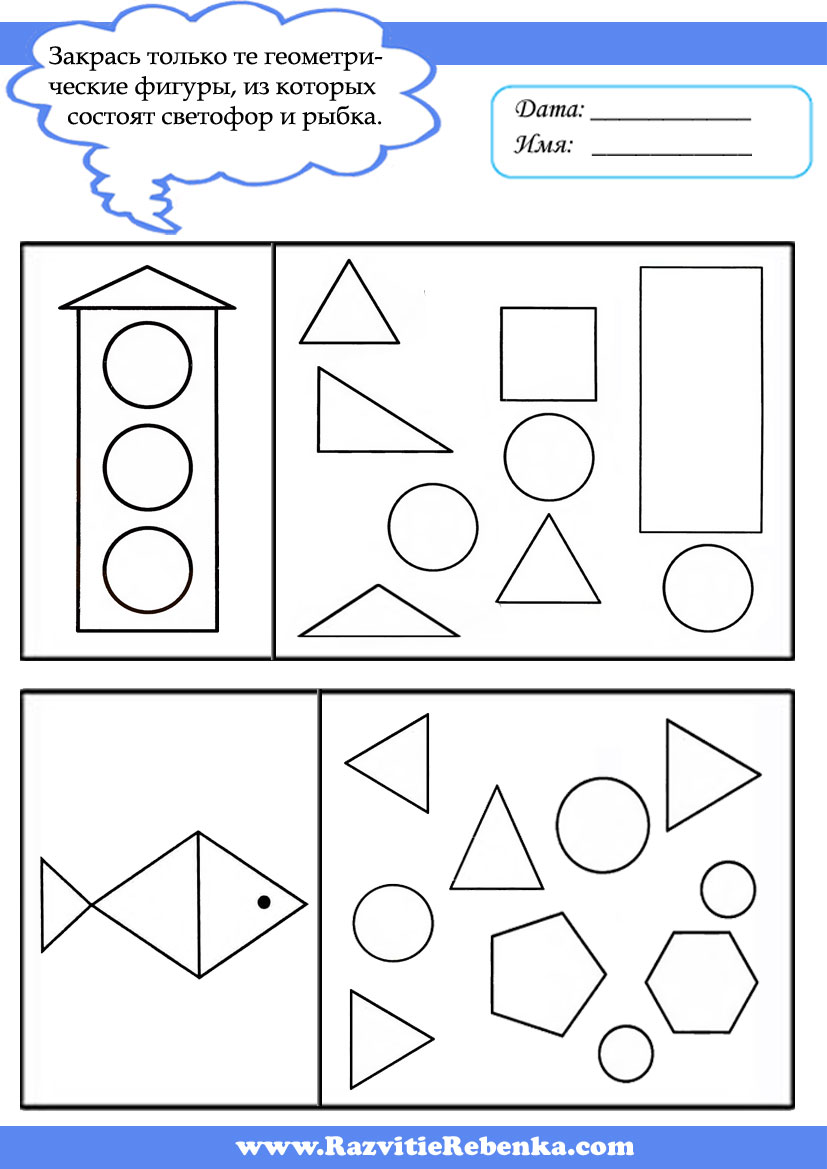  (овал).

Растянули мы квадрат

И представили на взгляд,

На кого он стал похожим

Или с чем-то очень схожим?

Не кирпич, не треугольник —

Стал квадрат… (прямоугольник)

Я фигура – хоть куда,

Очень ровная всегда,

Все углы во мне равны

И четыре стороны.

Кубик – мой любимый брат,

Потому что я…. (квадрат).

Воспитатель:

ТАРЕЛКА, ДВЕРЬ, КРЫША ДОМА, ОГУРЕЦ, ПЛАТОК.

Работаем на на листе простым карандашом .

Воспитатель: Какие фигуры у вас получились? Назовите их.

Дети: Круг, прямоугольник, треугольник, овал, квадрат.

Воспитатель: Как их можно назвать одним словом?

Дети: Геометрические фигуры .

Воспитатель: Сколько всего фигур?

Дети: 5

Воспитатель: Молодцы и с этим заданием вы справились без проблем.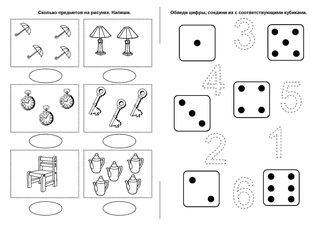

Игра «Ремонт моста»

– Ребята нам надо с вами перейти реку , но на ней разобран мост. Давайте отремонтируем его. На каждой дощечке есть цифра. Чтобы наш мост был крепким, дощечки с цифрами надо сложить по порядку, от 1 до 10. (Самостоятельная работа детей) .

– Проверим. Сосчитайте дощечки по порядку. Ничего не пропустили? (Нет) Теперь посчитайте в обратном порядке.

– Назовите, какая цифра стоит перед цифрой 6, 8, 10? (5, 7, 9.)

– Назовите соседей цифр 4, 6, 9? (3 – 5, 5 – 7, 8 – 10.)

Молодцы, все сделали правильно!

– Ребята, наш мост в порядке, а теперь присаживайтесь на свои места.

Воспитатель: Молодцы, вы очень хорошо справились с цифрами, и мы с вами заработали третью подсказку.

Пальчиковая гимнастика:

На моей руке пять пальцев,           повороты ладоней вверх-вниз

Пять хватальцев,

Пять держальцев.         

Чтоб строгать и чтоб пилить,                 имитируют движения

Чтобы брать и чтоб дарить.                 сжимают и разжимают кулачки

Их нетрудно сосчитать:                 пальцы – в замок

Раз, два, три, четыре, пять!                 выбрасывают пальцы из кулачков

(дети выполняют задание, оценивают

Игра «Рыбка плавает»

—М ы сегодня с вами будем дрессировщиками, но не обычными мы будем учить сегодня с вами плавать рыбку в разных направлениях и так приготовились:

• Рыбка плавает в середине пруда

• Рыбка поплыла в левый верхний угол

• Рыбка поплыла в правый нижний угол

• Рыбка вернулась опять в центр листа

• Затем поднялась вверх опустилась вниз

• Рыбка поплыла в левый нижний угол

Дальше она отправилась в правый верхний угол здесь ее путешествие заканчивается.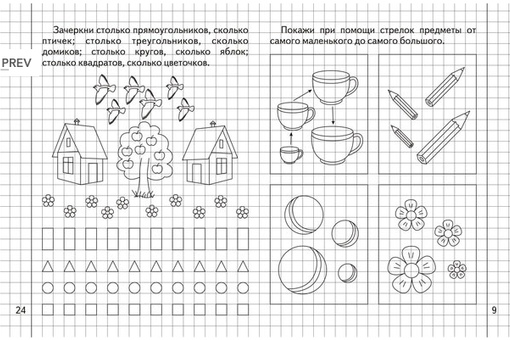

Молодцы ребята справились с заданием.

Воспитатель: Молодцы, вы очень хорошо справились с цифрами, и мы с вами заработали четвертую подсказку.

У вас на листочке нарисована подсказка, послушайте загадку:

«Ах, вы сладкие вкусняшки, что вы прячетесь в бумажки? Не получится, найдут! Вас они и выдают» (конфеты)

Давайте дорисуем конфету.

Теперь вы знаете какой сюрприз вас ждет.

Чтобы найти сюрприз, вы должны сделать 5 шагов вперед, 3 шага направо, 5 шагов налево и т.д.

(дети находят сюрприз).

Итог занятия:

Вам понравилось искать сюрприз и выполнять задания? Какие задания больше понравились? (ответы детей). 
А мне понравилось, что вы старались, и были очень активны. 
На этом занятие окончено.

Молодцы!

Муниципальное дошкольное образовательное учреждение

детский сад общеразвивающего вида №19 «Яблонька»

Конспект открытого занятия по математике (ФЭМП) в старшей группе «Путешествие в сказку.

Составила и провела:

Короткова Т.В.

с. Барановское

Московская область

2018г.

Неделя математики в ДОУ

Нужны ли занятия по математике в старшей группе детского сада?

Детский сад – это первое место, где ребенок начинает по-настоящему учиться. Конечно, получает знания он и дома, но в ДОУ обучение четко составлено методистами и спланировано. Так что если и говорят, что годы, проведенные в детском саду, — самые беззаботные, это только потому, что обучение там проводится в игровой форме. Если воспитатель сообщил вам, что в детском саду ребенка ждут занятия по математике (в старшей группе и средней это наиболее актуально), грамоте и даже английскому, не пугайтесь! Если говорить об арифметике, вашего ребенка просто-напросто научат считать в прямом и обратном порядке, различать цифры, понимать, что такое множество и т. д. В данной статье мы подробнее поговорим о том, что представляют собой занятия по математике в старшей группе, и приведем некоторые примеры.

Особенности обучения математике в старшей группе

Ваш ребенок пошел в старшую группу, он уже на пороге школы, а значит, необходимо дать ему базовые навыки всех основных для первоклашек предметов. В ДОУ вводить математику начинают в средней группе, там ребята учатся считать до пяти и узнают азы арифметики. Занятия по математике в старшей группе, в первую очередь, предполагают повторение уже изученного (4-5 уроков) и расширение материала. Продолжительность занятия увеличивается незначительно (с 20 минут до 25), однако количество информации вырастает в несколько раз. Исходя из этого, воспитатель должен следить за тем, как дети воспринимают информацию, и обязательно вводить игровые упражнения в план занятия. Вообще, нужно помнить, что уроки проходят с маленькими детьми, даже если это старшая группа. Занятие по математике лучше всего целиком сделать игровым. Тогда ни один ребенок, будь он с аналитическим или гуманитарным складом ума, не заскучает.

Занимательная математика в ДОУ

Старшая группа с радостью воспримет новый материал, оформленный в знакомые им реалии. Так, составляя план занятия, начните с интересного и увлекательного вступления. Мы приведем вам примерный план урока, который можно использовать не только для занятий в детском саду, но и дома.

Урок «Помоги мышатам»

Этот урок рассчитан на повторение счета до пяти и закрепление счета до десяти. Воспитатель делит группу на две команды и произносит вступление: «Сегодня я встретила двух мышат, они были очень голодными, а вы знаете, ребята, что мышата любят сыр.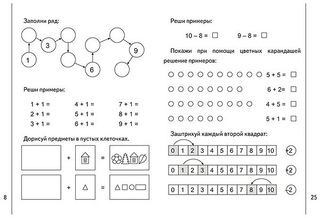 Давайте поможем им, я буду задавать вам задачки, а вы – отгадывать. За каждый правильный ответ команда получает кусочек сыра для своего мышонка». Воспитатель дает детям 5-6 задачек на счет. Вот примерные задания:

1. «Четыре серых кошки сидели у дорожки // А у каждой кошки по … ножки».
2. «Подарил мышатам ежик // Восемь золотых сережек // Кто мне скажет из ребят // Сколько было всех мышат?»
3. «Над рекой летали птицы: ворон, щука, три синицы, два ежа, пять голубей // Сколько птиц, ответь скорей!»

Дайте ребятам время сосчитать нужные предметы. Если возникают трудности, попросите их нарисовать то, что вы говорите, а после – сосчитать. Так будет развиваться и зрительное внимание. Не забывайте давать за каждый правильный ответ приз команде-победителю. В конце желательно, чтобы обе «мышки» получили свой обед.

Заключение

Вы можете использовать пособия для ДОУ либо придумать веселые задачки самостоятельно. Главное, дать понять ребенку и родителям, что занятия по математике в старшей группе – это не страшно, а весело и познавательно!

Конспект НОД по ФЭМП в старшей группе на тему «Путешествие в страну Математики»

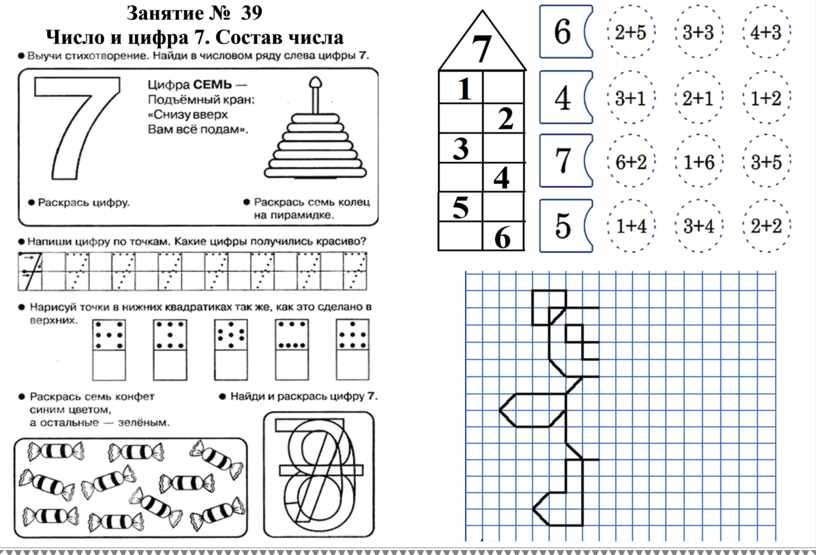
«Знакомство с числом и цифрой 6»

Цель: знакомство с числом и цифрой 6.

Задачи:

1. Учить отгадывать математическую загадку, записывать ее решение с помощью цифр и знаков.
2. Закрепить знания о числе 6 и познакомить с цифрой 6
3. Научить порядковому счету в пределах 6,правильно отвечать на вопросы сколько? На котором месте?
4. Знакомство с составом числа 6 из двух меньших
5. Учить решать задачу на установление закономерностей
6. Уточнить знания о насекомых, их образе жизни осенью.
7. Учить понимать учебную задачу и решать ее самостоятельно.
8. Формировать навык самоконтроля и самооценки.

Материалы и оборудование:

• цифры 3,4,5 по количеству детей для деления на группы;
• грибочки по 6 на команду, набор цифр-карточек от 1 до 6 и знаки +, =;
• числовой ряд над доской до 5 и цифра 6 для нового материала;
• игрушки или картинки — пчелы, комара, жука, муравья, кузнечика, бабочки;
• по листу бумаги на каждую команду с 1 нарисованной картинкой (мяч, яблоко, огурец), цветные карандаши.

План

1. Знакомства с Царевной Шесть, с её друзьями шестиногими насекомыми.
2. Деление на команды.
3. Реши задачку
4. Игра с мячом «Назови последующее число»
5. Физкультминутка «Бабочка».
6. Физкультминутка «Кузнечик».
7. Игровое упражнение «Ленивый художник».
8. Игровое упражнение «Кто, где спит зимой холодной?».
9. Самоконтроль и самооценка выполненной работы.

Ход занятия:

Организационный момент.

В группу входит Царевна шесть.

Царевна шесть: Здравствуйте ребята.

Дети здороваются.

Царевна шесть: Я Царевна шесть. Пришла к вам из страны арифметики. Мой брат Принц пять, рассказал мне, что в вашем детском саду есть ребята, которые умеют выполнять все задания. Я пришла попросить у вас помощи. Моих друзей-насекомых заколдовал Злой волшебник. Нужно выполнить задания, которые он придумал. Ребята, мне без вас не справиться. Поможете мне?

Дети: Да.

Основной этап

Царевна пять: Молодцы. Что бы справиться с заданиями Злого волшебника нужно разделиться на команды (делятся по цифрам 3, 4 и 5). Для этого волшебник даёт нам 1 минуту.

Дети делятся на команды

Царевна пять: Как хорошо, что мы успели вовремя. И первое насекомое будет расколдовано, а кто это узнаете, отгадав загадку -» Хлопотлива и смела, медоносная …» (пчела). Вот она.

Царевна выставляет на поднос пчелу или картинку размещает на доске.

Царевна пять: А сейчас очень трудное и сложное задание — надо решить задачу.

Реши задачку»

Задание: под березой выросла четыре грибочка, а под осиной вырос 1 грибочек. Сколько всего выросло грибочков? Выложите ответ на столе из грибочков и запишите решение при помощи цифр-карточек и знаков.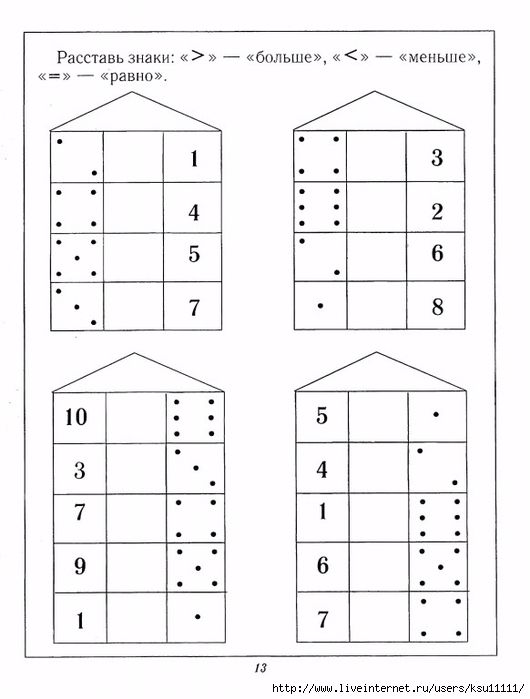

Ответы детей.

Царевна шесть: Верно, пять. Прошёл осенний дождик и на поляне вырос ещё один грибок. Сколько грибов стало на поляне? Добавьте к 5 грибочкам еще один.

Дети считают и называют.

Царевна шесть: Как получилось шесть?

Дети:к 5 добавили 1.

Царевна шесть: Выложите решение при помощи цифр-карточек и знаков.

Работа детей в командах.

Царевна шесть: Давайте проверим решение «сходив друг к другу в гости».

Дети проверяют.

Царевна шесть: Молодцы! Вы расколдовали второе насекомое «Черен — да не ворон, рогат — да не бык, шесть ног без копыт (жук). Вот и жук появился. Молодцы ребята!

Царевна шесть: Посмотрите, вот числовой ряд (до 5). Как вы думаете, где нужно расположить цифру 6?

Ответы детей: За числом 5, с правой стороны от 5.

Царевна шесть: Правильно, я поставлю на это место цифру 6.

Цифра 6 – дверной замочек,

сверху – крюк, внизу – крючочек.

Ребята, на что похожа цифра 6?

Высказывание детей.

Царевна шесть: И мы справились с еще одним заданием. Интересно. Кого мы расколдовали. «Не зверь, не птица, нос как спица, летит — кричит, сядет — молчит, кто его убьет — свою кровь прольет» Кто это? (комар). Вот и комарик.

Игра с мячом «Назови последующие число»

Царевна шесть: А в следующем задании нам поможет мяч. Я бросаю вам мяч и называю какое-нибудь число. Вы должны поймать мяч и бросить мне его назад, сказав число следующие за названным. Будьте внимательны. (1-…, 2-…, 4-… и т. д.)

Царевна пять: Молодцы! Смотрите кого мы расколдовали «Над цветком она порхает, пляшет, веером узорным машет». (бабочка). Какая красивая бабочка!

Царевна пять: А сейчас задание физкультурное.

Дети выполняют физкультминутки:

Физкультминутка «Бабочка»

Утром бабочка проснулась

Улыбнулась, потянулась

Раз – росой она умылась,

Два – изящно покружилась,

Три – нагнулась и присела,

На четыре – улетела.

Физкультминутка «Кузнечик»

Поднимайте плечики,

Прыгайте кузнечики,

Прыг – скок, прыг – скок,

Стоп! Сели!

Травушку покушали,

Тишину послушали.

Выше, выше, высоко

Прыгай на носках легко.

Царевна пять: вы так хорошо выполняли упражнения, что смогли расколдовать ещё одно насекомое — «На лугу живет скрипач, с ветки на тропинку, с травки на былинку, прыгает пружинка — зелёная спинка» (кузнечик).

Царевна шесть: Осталось последнее задание.

Воспитатель дает листочки, где нарисованы рисунки (например: в 1листочке нарисован 2 мяча, во 2 листке нарисован 3 огурца и т.п.).

Царевна шесть: Каждой команде нужно нарисовать на листе предметов столько, чтобы их стало по 6. Даю вам 1 минуту.

Дети рассказывают какие предметы они нарисовали и сколько их стало.

Царевна шесть: И с этим заданием мы справились! Кого же мы расколдовали? «Больше собственного веса

Тащит этот житель леса,

Груз родной семье своей,

Он зовется……» (муравей).

Царевна шесть: Ребята. Какие вы молодцы! Вы расколдовали моих друзей-насекомых. Сколько их?

Дети считают.

Заключительный этап

Царевна шесть: Спасибо вам. Вы мне очень сильно помогли. А вы знаете, где спят мои друзья насекомые зимой?

Ответы детей. Если дети затрудняются ответить, педагог помогает.

Игровое упражнение «Кто, где спит зимой холодной?»

• Комар как и стрекоза зимует в стадии личинки.
• А вот пчелы зимой не спят, они становятся очень медлительными и вялыми. В природе пчёлы селятся в дуплах деревьев.
• Муравьи роют себе убежище от мороза на глубине свыше метра, там, где температура держится одинаковая.
• Кузнечики зимуют в земле в стадии яйца, весной из яиц появятся личинки, а к лету будут настоящие кузнечики.
• Бабочки забиваются в укромные места в дупла деревьев, в кору деревьев, на крыши домов.

Ответы детей. Царевна шесть прощается с ребятами.

Рефлексия

— С какой цифрой вы познакомились?
— Какие задания вам больше понравилось выполнять.

Скачать — Конспект занятия НОД по математике в старшей группе по теме: «Знакомство с числом и цифрой 6»

Автор: Шигабутдинова Лиана Раилевна
Должность: воспитатель первой квалификационной категории
Место работы: Муниципальное казенное дошкольное образовательное учреждение детский сад компенсирующего вида № 1 «Ручеек» города Вятские Поляны Кировской области
Месторасположение: Кировская область, г. Вятские Поляны, улица Центральный микрорайон, 3а

Дата изменения: 30. 10.2018
Дата публикации: 30.10.2018

Конспект занятия по математике в старшей группе «В гостях у сказки»

Конспект занятия по математике в старшей группе «В гостях у сказки»

Корниенко Елена Викторовна Воспитатель 1 квалификационной категории МКДОУ «Лемешкинский детский сад «Солнышко» Волгоградская обл. Руднянский р-н

Образовательные задачи

• научить выполнять задание согласно заданной схеме.
• решать логические задачи
• закреплять навыки порядкового счета в пределах 10 (прямой и обратный счет)
• закрепить знание геометрических фигур
• закреплять умение детей ориентироваться в пространстве; —учить решать простые задачи на сложение и вычитание

Развивающие задачи:

• Развивать логическое мышление, память, внимание, умения выдвигать гипотезы, делать выводы, выбирать способ действия;
• обогащать и расширять словарь детей. .

Воспитательные задачи:

• Воспитывать интерес к математике, учить доводить начатое дело до конца;
• воспитывать дружеские взаимоотношения, доброжелательность, взаимопомощь в ходе игры, желание прийти на помощь. Развивать умение работать вместе,
• уважать мнение партнера, не перебивать говорящего.

Краткое описание: проводится с детьми старшей группы по занимательному сюжету в виде путешествия. Закрепляются такие понятия, как: порядковый счет, обратный счет, цвет, форма, геометрические фигуры.

Ход занятия

Звучит музыка «В гостях у сказки»

Воспитатель входит в группу с зонтом. Посмотрите, что у меня есть. Что это? Правильно — это зонт. А зонт у меня необыкновенный и подарил мне его необыкновенный сказочник и волшебник

Загадка:

Приходит он глубокой ночью,
И зонтик свой волшебный открывает.
Зонт разноцветный – сон ласкает очи,
Зонт чёрный – снов в помине не бывает.

Послушным детям – зонтик разноцветный,
А непослушным – чёрный полагается.
Он гном-волшебник, многим он известный.
А ну, скажи, как гном тот называется? (Оле Лукойе)

Кто знает кто такой ОЛЕ ЛУКОЙЛЕ? Никто на свете не знает столько сказок, сколько знает их Оле Лукойе. Под мышками он носит по зонтику: один с картинками, его он раскрывает над

хорошими детьми и рассказывает добрые сказки, а другой тёмный, который Оле Лукойе развёртывает над нехорошими детьми. Какой зонт подарил мне Оле Лукойле?

Мне Оле Лукойле дал цветной зонт- значит вы очень хорошие дети

Солнце на небе проснулось,
Нам, ребята, улыбнулось.
Глазки тихо закрываем,
Руки к небу поднимаем,

Лучи солнышка возьмем
И к сердечку поднесем.

Смотрю я на ваши лица, они сияют от радости и, я надеюсь, что это настроение у нас сохранится в течение всего дня и сказка, которую нам подарит зонтик будет тоже добрая, поучительная. А вы любите слушать сказки? Ну, а сами не хотите попасть в сказку и помочь сказочным героям? С помощью зонтика, я хочу вам рассказать сказку, сказка не простая, волшебная, с математическими заданиями. Я давайте сегодня не только послушать сказку, но и отправиться в сказочное МАТЕМАТИЧЕСКОЕ ПУТЕШЕСТВИЕ, где мы будем считать и отсчитывать предметы, выполнять логические задания, будем учиться ориентироваться в пространстве, вспомним дни недели.. вспомним нужно закрыть глазки

Чтобы попасть в сказку я раскрываю красивый зонтик, а вы закрывайте глазки. Я буду крутить зонт, и говорить волшебные слова.

Волшебство сейчас начнется, Стоит зонтик нам раскрыть, Зонтик раскрывается, глазки закрываются

Сказка начинается. Мы сильней его покрутим, Вот и в сказке тут же будем!

Воспитатель: Дети, вы любите слушать сказки?

II. Основная часть. (выставить картинку Ивана Царевича)

Воспитатель: Открывайте глаза. Мы с вами в самой настоящей сказке. Сказка начинается. (музыка в гостях у сказки)

Жил-был Иван-Царевич. И была у него невеста – Елена Прекрасная. Однажды гуляли они в роще, и вдруг налетел вихрь и унес Елену. Опечалился Иван-Царевич, сел на землю, залился горючими слезами. А березка над ним шелестит и говорит человеческим голосом: «Не плачь, добрый молодец, найдешь ты свою невесту у Кощея Бессмертного в Математической стране».

И решил Иван Царевич отправиться в далекий путь. А вы хотите пойти с Иваном Царевичем? Трудная дорога выдалась. Идём, по непроходимому лесу- ветки раздвигаем, через коряги перешагиваем. Долгим и трудным был путь и вот на пути встретилась река. Как же перебраться на другой берег? Здесь нет ни мостика, ни лодочки.

Дети: Вплавь, вброд.

Воспитатель: Нет, уже осень, вброд нельзя, вода холодная, можно простудиться. Давайте потрогаем воду руками (пальчиками шевелим в «воде») и покажем, как можно замерзнуть в этой воде (дети мимикой и движениями изображают холод).

Воспитатель: Подождите, подождите, здесь что-то есть. А, понятно, это схема моста. Видимо, его просто не успели построить. Вот и материал для сооружения моста. Сможет Иван Царевич построить мост– значит, перейдет через реку, а не сможет – не выручит свою царевну. Поможем Ивану-Царевичу справиться с заданием?

Давайте сделаем доброе дело, возьмем по одной детали и построим мост.

(Дети берут детали).

Воспитатель: Ребята, назовите свои детали.

Воспитатель спрашивает у нескольких детей, какая геометрическая фигура у них в руках и какого она цвета.:. Все внимательно посмотрите на схему и, не теряя времени, принимайтесь за строительство.

Дети, согласно рисунку, выкладывают плоскостные геометрические фигуры.

Когда «мост» закончен, дети друг за другом на носочках переходят на другую сторону.

Воспитатель С вашей помощью Иван-Царевич благополучно миновал реку, пришёл к избушке Б. Я.

Вошёл И.Ц. в избушку, а там на печи, на девятом кирпичи сидит Б.Я. – рассказал он ей про свою беду, а старушка была хитрющая, любила разные вопросы и загадки загадывать. Говорит Яга: «Пока на вопросы не ответишь, разговаривать не стану.» Задумался Царевич. А вдруг не ответит? Ребята, давайте мы поможем Царевичу ответить на вопросы

• Назовите дни недели.
• Назовите выходные дни.
• Какой день идёт за понедельником
• Какой день идёт за средой
• Как называется пятый день недели
• Как называется день перед средой

Воспитатель: Молодцы, ребята, помогли вы Царевичу. «Вот теперь, — говорит Баба Яга, — могу дать тебе волшебный клубочек, который укажет дорогу к Кощею». – «Нет, — говорит Иван-Царевич, — мне надо скорее. Дай мне лучше ступу». «Что ж, бери. Да только у меня их несколько, все в беспорядке стоят. Вот расставь их по порядку- по номерам, тогда и выбирай.

(обклеить стаканы с цифрами)

Воспитатель: Давайте разберемся со всеми ступами:

• Расставить ступы по прядку. Счёт в прямом и обратном порядке до 10.
• Между какими по счёту ступами стоит ступа под номером 5? (4 и 6)
• Между какими по счёту ступами стоит ступа под номером 7? (6 и 8)
• Какая по счёту стоит зелёная ступа?
• Какая по счёту стоит красная ступа?
• На каком месте стоит синяя?
• На каком месте стоит жёлтая.?
• Так какую ступу выбери для И.Ц.

Расставили мы Б.Я. ступы по прядку, по номерам, а она сказала, что смерть Кащея в игле, игла в шкатулке, а шкатулка под троном лежит.

Воспитатель: Поблагодарил Иван Бабу-Ягу, сел в ступу и через полминуты приземлился около огромного камня, который лежал на развилке дорог. Сделать из бумаги

Призадумался Иван, не знает, в какую сторону ехать двигаться. Тут кто-то человечьим голосом: «Выполни задания, что на камне написаны, тогда тебе и направление покажется.» На камне нацарапано что-то, а Царевич то в школу не ходил, читать не умеет. Что делать- хоть назад возвращайся- да нельзя Царевну выручать надо. Ребята, а я читать то могу- вот прочитаю и поможем — давайте присядем на поляну и ответим на вопросы

(сесть на палас)

• Если стол выше стула, то стул… (ниже стола).
• Если дорога шире тропинки, то тропинка… (уже дороги).
• Если два больше одного, то один… (меньше двух).
• Если сестра старше брата, то брат… (младше сестры).
• Если правая рука справа, то левая… (слева).
• Если лента длиннее шнурка, то шнурок… (короче ленты).

Смотрите –ответили мы на вопросы и появилась- стрела красная. Давайте её запустим и направление куда идти узнаем. Запускаем стрелу в сторону????

Обрадовался Иван Царевич, что нашел нужную дорогу. Но прежде чем идти к Кощею, я предлагаю немножко размяться.

Физкультминутка

Мы сейчас все дружно встанем.
Ноги шире мы поставим.
Вправо, влево повернуться,
Наклониться и подняться.

Руки вверх, руки вбок,
И на месте прыг да скок.
А теперь мы шагаем дружно
Царевичу помочь нам нужно.

Увидел Кощей Бессмертный, что идет к нему Иван-Царевич, и решил притвориться добреньким, а сам задумал дело хитрое. Тем временем Иван-Царевич вошел уже во дворец. Появился наш герой перед Кощеем, а тот ему говорит так ласково: «За невестой пришел, добрый молодец? Давай мирно договоримся: задам я тебе всего одно задание. Справишься- забирай Елену Прекрасную, а не справишься – голова твоя с плеч долой». Делать нечего, согласился Иван. Говорит Кощей: «купил я себе мебель новую- расставь мне её, как я скажу»

• В правом верхнем углу стоит кровать
• В левом нижнем углу стоит шкаф
• В центре комнаты стоит стол
• В левом верхнем углу стоит телевизор
• В правом нижнем углу стоит диван
• (распечатать предметы мебели на каждого ребёнка)

Воспитатель: Решил Иван-Царевич задачу, но не захотел Кощей Бессмертный выполнить свое обещание. Выхватил тогда Иван меч, и стали они сражаться. Шаг за шагом все ближе и ближе подбирается Иван к трону. Вот уже и схватил он шкатулку с иглой. На шкатулке – задачи. Не решив задачи, шкатулка не откроется.

Презентация — задач

Воспитатель: Помогли мы с Ивану –Царевичу решить задачи, в тот же миг шкатулка открылась. Иван взял в руки иглу и переломил ее. Кощей упал замертво, а стена, за которой Царевну Кащей рухнула и увидел И.Ц. около яблоньки свою невесту Елену Прекрасную. (купить в жирновске или распечатать)

Стал Иван-Царевич рассказывать о своих приключениях, о том, с какими трудностями пришлось ему встретиться на пути к невесте, и предложил ей свою руку и сердце. Елена Прекрасная восхитилась Иваном и согласилась выйти за него замуж. Отправились они домой, в свое царство.

А нам тоже пора возвращаться. Если вам в сказке понравилось, сорвите с яблоньки красное яблоко, а если не понравилось-то зелёное.

Давайте возьмём зонтик и перенесёмся назад в свою группу.

Волшебство сейчас начнется, Стоит зонтик нам раскрыть, Зонтик раскрывается, глазки закрываются

• Мы сильней его покрутим, Вот и в группе тут же будем!

III. Заключительная часть

Воспитатель: Вот и закончилась сказка.

— А теперь покажите кто какое яблоко сорвал. красное -кому понравилось в сказке?

— что понравилось?

— А чему она учит? (Добру, взаимопомощи)

— Какие трудности пришлось преодолеть Ивану Царевичу?

— Справился бы он без нашей помощи? (Нет)

Про зелёные яблоки

Воспитатель. Мне тоже очень понравилось в сказке. а я тоже нарвала яблок с дерева. Я нарвала красные яблоки, п.ч. вы все молодцы…

НОД по развитию математических представлений в подготовительной группе «Игра-путешествие в страну Математики»

Автор:

Офицерова Любовь Анатольевна,

воспитатель МБДОУ ЦРР-ДС «Крепыш»

города Ноябрьска

Цель: развитие интереса к предмету математики, на основе познавательной активности и любознательности.

Задачи:

Образовательная. Способствовать формированию умения применять математические знания в нестандартных практических задачах.

Развивающая. Развивать мыслительные операции: аналогия, систематизация, обобщение, наблюдение, планирование.

Воспитательная. Содействовать поддержанию интереса к математике, формированию умения трудиться в коллективе.

Материал:

Карандаши, фломастеры, листы бумаги, Телеграмма от Феи из волшебной Страны Математики, числовой ряд, карточки с числовыми неравенствами, карточки с точками и цифрами, счетные палочки, сюрприз (звездочки), магнитная доска.

Место проведения: групповая комната.

Предварительная работа:

Знакомство с математическими сказками, стихами, загадками. Разучивание физ. минуток, настольные игры. Разучивание стихов математического содержания

1 часть Введение в игровую ситуацию:

Воспитатель: Ребята, сегодня утром, почтальон вручил мне телеграмму, адресованную нашей группе. Давайте  ее прочитаем

Телеграмма:

 «Здравствуйте дорогие ребята, пишет вам Фея  из Страны  Математики . Я приглашаю вас в Страну Математики. Но путь в эту страну будет нелегким. Чтобы в нее попасть, нужно много знать .А чтобы показать свои знания, вам нужно выполнить  задания. Тот, кто справиться с этими заданиями, получит приз»

Воспитатель: Ребята, вы хотите попасть в Страну  Математики?

Дети: Да.

Воспитатель: Тогда давайте подготовимся к путешествию и проведем разминку для ума.

Воспитатель: Ребята, для того, чтобы ответить правильно, нужно внимательно слушать:

—  счет от заданного числа до 10;

—  обратный счет от 10 до 0;

—  назови число, которое больше 4, но меньше 6;

—  назови число, которое больше 5, но меньше 7;

—  назови числа, стоящие в ряду справа от 5;

—  назови соседей числа 4, числа 6, числа 8;

—  назови число, которое стоит перед числом 6;

—  назови число, которое следует за числом 8;

—  если дорога шире тропинки, то тропинка…(уже) дороги;

—  если линейка длиннее карандаша то карандаш…(короче) линейки;

—  если верёвка толще нитки, то нитка …(тоньше ) верёвки;

2 часть . Воспитатель: Молодцы ребята, вы очень хорошо подготовились к путешествию.  На чём же мы отправимся?

—  Чтобы узнать какой транспорт нам понадобиться, нужно соединить на листах точки по порядку. И получится картинка. Я дам вам небольшую подсказку, загадаю  загадку.

Загадка: Чудо-птица синий хвост прилетела в стаю звёзд? (ракета) 

Воспитатель: Молодцы вы справились с заданием, но что бы ракета взлетела, нам нужно выполнить следующие задание:

—  На доске записаны числовые выражения

8+1=          7+2=         4+5=           2+7=         6+3=            8 — 4=

Воспитатель: Среди этих чисел есть одно лишнее. Как его найти? Как вы будите выполнять  задание?

Дети: Сначала нужно решить числовые выражения, а потом найти лишнее число.

Воспитатель: Молодцы, ребята. Наша ракета готова к взлёту. Полетели .

1 остановка: Задачкина

Воспитатель: У феи живут самые разные животные и птицы, и они любят придумывать разные задания для путешественников. Они предлагают вам поработать в парах и придумать задачу по числовому примеру (карточки с примерами на столах у детей).

-Давайте вспомним, из каких частей состоит задача?

Дети: Задача: условие——-вопрос——решение ——ответ.  

Воспитатель:  Если в задаче из целого удаляется часть. Становится мешьше, чем было и требуется найти остаток, каким действием решается такая задача?

Дети: Вычитанием

Воспитатель: Вычитание – это значит, что нужно увеличить  или уменьшить?

Дети: Уменьшить.

Уменьшить, чтобы найти оставшуюся часть.

Воспитатель:  Если в задаче объединяются части. Становится больше, чем было, каким действием решается задача?

Дети: Сложением.

Воспитатель:  Сложение — это значит, что нужно увеличить  или уменьшить?

Дети: Увеличить. Объединить части и найти целое.

Дети за столами с помощью числовых карточек составляют и  решают задачи.

Воспитатель:  Чтобы легче было работать, проведём разминку.

Физкультминутка.

Раз – нагнуться, разогнуться.

Два – нагнуться, потянуться.

Три – в ладоши три хлопка,

Головою три кивка.

На четыре – руки шире.

Пять, шесть – тихо сесть.

Воспитатель:  Следующее остановка: Геометрическая.

Составление геометрических фигур с помощью счётных палочек:

—  составить 2 равных треугольника из 5 палочек. 

—  составить 2 равных квадрата из 7 палочек.

—  составить 3 равных треугольника из 7 палочек

—  составить 4 равных треугольника из 9 палочек.

—  составить из 9 палочек квадрат и 4 треугольника.

Воспитатель: Следующее остановка: Числовая.  Вам нужно правильно расставить знаки

 « больше», « меньше» или  «равно» 

3 часть. Итог .Награждение  наиболее активных детей  звездочками

Постановка новой проблемы.

Воспитатель: А кто скажет, зачем нужна Математика?

(Ответы детей)

Воспитатель: Кому она нужна?

(Ответы детей)

Воспитатель: Хотите больше узнать о Математике, о том кому она нужна?

Хорошо. Об этом мы с вами поговорим позже.

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. 1. Л.Г. Петерсон, Н.П.Холина «РАЗ- ступенька, ДВА – ступенька»    Методические  рекомендации. Практический курс математики для дошкольников. Москва2009 г.
2. Г.М. Лямина «Подготовительная к школе группа в детском саду. М..,  « Просвещение», 1975г.
3. Т.И. Ерофеева «Дошкольник изучает математику» М…, «Просвещение»2009г.
4. М. В. Ильина «Тренируем внимание и память. М…, 2005г.
5. 5.С.В. Бурдина «Задания на развитие зрительного восприятия»

«Свидетельство о публикации в СМИ» Серия А № 0002332

Штрих код (№ квитанции) 62502670051776  Дата отправки 22 января 2014 г.

Приглашаем педагогов дошкольного образования Тюменской области, ЯНАО и ХМАО-Югры опубликовать свой методический материал:
— Педагогический опыт, авторские программы, методические пособия, презентации к занятиям, электронные игры;
— Лично разработанные конспекты и сценарии образовательной деятельности, проекты, мастер – классы (в т. ч. видео), формы работы с семьёй и педагогами.

Почему выгодно публиковаться у нас?

1. «Детские сады Тюменской области» официально зарегистрированное профильное СМИ федерального уровня. ЭЛ № ФС 77 — 43321
2. Деятельность редакции поддерживается Департаментом образования и науки Тюменской области
3. Мы оформляем «Свидетельство о публикации» в СМИ.
4. Документ имеет уникальный номер, вписан в реестр, имеет оригинальную печать редакции интернет-издания и подпись.
5. «Свидетельство о публикации» в СМИ отправляется автору как в бумажном, так и в электронном варианте.

Подробно >>>

Образец «Свидетельства о публикации авторского методического материала в СМИ».pdf

Проекты — Факультет математики

Прошлые проекты

2020 Студенческие проекты

2019 Студенческие проекты

2018 Студенческие проекты

2017 Студенческие проекты

2016 Студенческие проекты

Научные интересы преподавателей

Преподаватели математического факультета колледжа Джорджии имеют исследовательские интересы в различных областях математики и математического образования. Следующие описания преподавателей дают учащимся представление об этих интересах по отношению к руководству проектами старших классов.

научных интересов доктора Анхеля Эбни включают в себя модели математики учащихся для будущих учителей, эффективность подготовки учителей для будущих учителей, математические знания для обучения, математические знания, необходимые для обучения учителей, и удержание женщин и меньшинств в математическом конвейере.

областей интересов доктора Марты Аллен включают теорию чисел и криптографию.Предыдущие проекты включали изучение набора доказательств бесконечности простых чисел и исследование того, почему простые числа важны, исследование влияния шифров на Первую и Вторую мировые войны, исследование современного применения теоремы Эйлера и рассмотрение приложений примитивных корни и дискретные логарифмы в криптографии. Студент, желающий работать над проектом с доктором Алленом, должен демонстрировать сильную трудовую этику, быть очень мотивированным, свободно писать математические записи и владеть LaTeX. Кроме того, для проведения исследований в области теории чисел учащийся должен успешно пройти курс МАТЕМАТИКА 4110, а для проведения исследований в области криптографии учащийся должен пройти или одновременно проходить курс МАТЕМАТИКА 4110, будучи зачисленным в курс МАТЕМАТИКА 4989.

 научных интересов доктора Гая Бийогмама в основном лежат в области неассоциативных алгебр в сочетании с такими областями, как алгебра Лейбница, алгебраическая топология, гомология Лейбница, теория инвариантов и гомологическая алгебра. Возможные проекты будут заключаться в использовании спектральной последовательности Пирашвили для обнаружения (не)релятивистских инвариантов, которые могут быть полезны при вычислении (ко)гомологий Лейбница абелевых расширений полупростых алгебр Лейбница.Он также проявляет некоторый интерес к BCK-алгебрам, стойкам, теории нечетких множеств и полилинейным алгебрам Ли. Эти поля могут генерировать несколько проектов бакалавриата. Некоторые проекты под моим руководством, которые я могу просмотреть: «Исследование подстоек» (American Journal of Undergraduate Research, 13 (2) (2014), 19–27) и «Центры некоторой нерелятивистской алгебры Ли» (Роуз-Халман Бакалавриат). Математический журнал, том 16, выпуск 1, 2015 г.).

 Научные интересы доктора Джорджа Казаку включают общую топологию, динамические (поли)системы и теорию устойчивости, а также сложность алгоритмов.Он решает проблему P и NP в надежде, что однажды он сможет полностью понять ее. У студента, заинтересованного в исследованиях под его руководством, будет большой выбор тем, варьирующихся от строгого понимания абстрактных топологических понятий до изучения открытых проблем или особых, менее изученных случаев аттракторов в динамических (поли)системах или изучения некоторые проблемы с НП.

областей научных интересов доктора Марселы Чиореску включают абстрактную алгебру и ее приложения (в частности, коммутативную алгебру), историю математики (в частности, историю математики в Японии и Китае) и связь между математикой и искусством. (в частности связь между математикой и темари).Студент, желающий работать над проектом в любой из этих областей, должен успешно завершить как минимум MATH 3030 и владеть LaTeX.

Основной областью научных интересов доктора Рэйчел Эпштейн является математическая логика и, в частности, теория вычислимости. Кроме того, ее интересуют связи между математикой и оригами, история математики во всем мире и применение математики к социальным вопросам, таким как мошенничество и голосование.Если говорить больше о теории вычислимости, то это исследование того, что можно вычислить с помощью теоретического идеализированного компьютера (или машины Тьюринга), а что нет. В области невычислимого мы можем классифицировать математические объекты, такие как действительные числа, по тому, сколько информации они содержат. Теория вычислимости может применяться ко многим областям математики, таким как абстрактная алгебра или теория графов, а также изучаться сама по себе. Для работы над проблемами теории вычислимости единственным предварительным условием были бы «Основы математики» (MATH 3030).Подобласть теории вычислимости, тесно связанная с информатикой, — это изучение случайности. Для работы со случайностью была бы полезна Вероятность (MATH 4600). Другие темы математической логики включают теорию множеств, теорию моделей и теоремы Гёделя о неполноте. Учащиеся, интересующиеся информатикой, философией, психологией или физикой, могут работать над темами, сочетающими теорию вычислимости или математическую логику с этими дисциплинами.

Доктор Сусмита Садху занимается исследованиями динамических систем (дифференциальных уравнений) и их приложений.В частности, ее исследования можно разделить на две группы: (i) изучение и интерпретация поведения решений нелинейных краевых задач (которые представляют собой обыкновенные дифференциальные уравнения с наложенными на них определенными граничными условиями), (ii) качественный анализ и геометрический анализ. визуализация решений систем дифференциальных уравнений, моделирующих некоторые физические, биологические или экологические явления. Студенту, заинтересованному в изучении классической теории дифференциальных уравнений или интересующемся изучением задачи, моделирующей экологический или биологический процесс, должен быть удобен материал из одного из вышеперечисленных наборов. Математические инструменты, такие как Maple, MATLAB, XPPAUT, будут часто использоваться и обучаться студенту. Желательны, но не обязательны навыки программирования. Заинтересованным студентам настоятельно рекомендуется просмотреть некоторые студенческие журналы, чтобы получить представление о характере исследований, проводимых в этой области. Вот некоторые возможные документы, которые можно просмотреть: «Модель хищника-жертвы с динамикой болезней» (Математический журнал Роуза-Халмана для студентов, том 4, выпуск 1, 2003 г.), «Долгосрочная динамика двух трехвидовых пищевых сетей» (Роуз-Халман). Журнал бакалавриата по математике, том 4, выпуск 2, 2003 г.) и «Представление падальщика в модели хищника-жертвы» (электронные заметки по прикладной математике, 2007 г.) и т. д.

областей интересов доктора Брэндона Сэмплса включают теорию представлений (представление объектов с помощью методов линейной алгебры), абстрактную алгебру, теорию чисел, теорию графов и математическое образование. Студент, желающий работать над проектом с доктором Сэмплсом в условиях чистой математики, должен быть заинтересован и чувствовать себя комфортно с материалом, по крайней мере, из подмножества вышеупомянутых разделов математики. Поиск журналов по математике для студентов (Rose-Hulman, College Math Journal и т. д.).) должен позволить учащемуся сформулировать некоторые возможные темы. Предыдущие проекты включали темы, исходящие из изучения алгебр Ли, связанных с конечными группами, комбинаторики конечных графов, обобщенных последовательностей Фибоначчи и обобщений проблемы Фробениуса в теории чисел. Студент, желающий работать над проектом в области математического образования, должен был подумать о возможных темах и изучить литературу, чтобы получить представление о возможной структуре. Для начала учащийся должен был уже просмотреть некоторые документы по математическому образованию, чтобы получить представление о характере исследований в области математического образования.Предыдущие проекты включали анализ концептуального и процедурного понимания в контексте сюжетных задач, а также оценку эффективности различных обучающих манипуляций на уровне бакалавриата.

Научные интересы д-ра Дорис Сантароне лежат в области математических знаний для обучения учителей без отрыва от работы и будущих учителей, знаний по математике для будущих учителей и учителей без отрыва от работы, математических знаний, необходимых для учителей-преподавателей, а также оценки проектов и программ. для подготовки учителей математики.

Доктор Симплис Чамна основной областью интересов является абстрактная алгебра. Он интересуется вопросами коммутативной алгебры. Коммутативная алгебра — это область математики, изучающая коммутативные кольца и другие связанные темы, такие как теория модулей. Многие области современной математики, такие как теория чисел, гомологическая алгебра, алгебраическая геометрия и т. д., используют результаты коммутативной алгебры. Студент, желающий работать с ним, должен пройти (с оценкой не ниже C) два курса Math 3030 (Основы математики) и Math 4081 (Абстрактная алгебра).Он также доступен для работы со студентами, желающими изучить темы статистики. Он интересуется методами сбора данных для прогнозирования. В этом случае студент должен пройти два курса Math 1262 (Исчисление I) и Math 2600 (Вероятность и статистика).

 Научные интересы д-ра Хун Юэ связаны с гармоническим анализом, связанным с функциональными пространствами, дифференциальными уравнениями, фрактальной геометрией и решением проблем. Студенты, которые хотят работать над проектом с Dr.Юэ должен был пройти курс МАТЕМАТИКА 3030, Основы математики. Кроме того, если они заинтересованы в проекте по чистой или прикладной математике, они должны пройти хотя бы один из курсов МАТЕМАТИКА 4340, Дифференциальные уравнения и МАТЕМАТИКА 4261, Математический анализ. Также приветствуется, чтобы учащиеся хорошо владели компьютерным языком или математическим программным обеспечением, в частности, если они интересуются темой дифференциальных уравнений или фрактальной геометрии.

старший проект | Математика | Luther College

Старший проект по математике должен стать кульминационным, независимым опытом основной математики. Студенты должны выбрать члена факультета математики, который будет их руководителем. Посоветовавшись с этим научным руководителем, студент должен выбрать математическую тему для изучения в старшем проекте. Проект должен быть представлен в письменном виде, а также в публичной устной презентации.

Старшее проектное предложение

Учащиеся, желающие выполнить проект по математике для старшеклассников, должны подать форму предложения по проекту для старшеклассников, которая должна быть одобрена кафедрой математики.

Приведенная выше форма предложения должна быть заполнена до второй пятницы семестра, в котором будет завершен проект для старшеклассников. Вам потребуется одобрение вашего руководителя проекта, прежде чем завершить форму вашего предложения, поэтому настоятельно рекомендуется начать этот процесс намного раньше установленного срока!

Последние названия проектов старшего курса по математике

Ниже приводится список некоторых последних названий старших проектов, который может дать вам некоторое представление о характере того, что можно изучать для старшего проекта.

Математика

• Математика музыкальных инструментов
• Комбинаторная теория игр Нима
• Модель приземного климата как функция времени и широты
• Метод прямых по уравнению Лапласа
• Теория групп и абстрактная алгебра в головоломках
• Криптография: от Caesar до Enigma и от RSA до наших дней
• Фурье-анализ музыкального тембра
• Моделирование возможностей бейсбольного шлема для предотвращения травм головы
• . Разностные множества и теорема Маскетти
.
• Математический анализ алгоритма быстрого компьютера Фурье
• Математическая модель производства мусора в Delmas 33, Zone Siloe с использованием обыкновенных дифференциальных уравнений
• Вот как звучит математика: математическое моделирование человеческого уха
• Оптимальный контроль эпидемий лихорадки денге
• Алгоритмы квантовых вычислений
• Леонард Эйлер: жизнь и (некоторые) работы
• Китайская теорема об остатках и ее применение к алгоритму RSA
• Введение в криптографию на основе эллиптических кривых
• Манхэттенское восприятие расстояния
• Идеальные перетасовки и результирующие перестановки
• Теория кодирования
• Кубик Рубика и теория групп
• Три теоремы о нестандартных костях
• История Великой теоремы Ферма и введение в эллиптические кривые
• Символы Лежандра и их применение в подбрасывании монет
• Математика контрольных цифр

Математика/Статистика

• Анализ характеристик массы груди и их диагностика с использованием множественной логистической регрессии, перекрестной проверки и другого статистического анализа
• Статистический анализ результатов и прогнозов фэнтези-футбола
• Модель для прогнозирования качества и цвета вина
• Количественная оценка объема подходящей среды обитания для миграции чавычи и стальноголового лосося вниз по течению в верховьях водохранилища озера Шаста, Калифорния
• Статистический анализ факторов глобального потепления в сравнении с регионами мира
• Прогнозирование вероятности текучести кадров в мужском колледже Ultimate
• Бери копейки, оставляй копейки: статистический анализ мелочи
• Влияние различных доз кофеина на выносливость и исследование содержания кофеина в газированных напитках
• Поиск прогнозных индикаторов процента побед в Высшей лиге бейсбола
• В минусе: статистический анализ долга бакалавриата за 2012–2013 годы
• Модель множественной линейной регрессии для определения времени выживания пациентов с первичным билиарным циррозом.
• Диагностика СДВГ и характеристики состояния в классе.

Старших проектов по математике | Тихоокеанский университет

Ниже приводится подборка проектов для старших классов по математике.

2018

Бренна Успокаивающая

Симметрия и структура: характеристика графов автоморфизмами и фиксирующими числами

Подмножество S вершин графа G является фиксирующим множеством для G тогда и только тогда, когда тождественный автоморфизм является единственным автоморфизмом G, который фиксирует каждую вершину S.То есть каждый автоморфизм G полностью определяется своим действием на фиксирующем множестве S. Фиксирующее число G, обозначаемое fix(G), является мощностью наименьшего фиксирующего множества G. Группы автоморфизмов и фиксирующие числа позволяют нам описывают свойства симметрии и структурную сложность графа. Мы начнем с изучения групп автоморфизмов и фиксации чисел различных классов конечных простых графов. Затем мы доказываем два результата о дополнениях к графам, которые позволяют нам утверждать, что все результаты о фиксированных числах для несвязных графов также должны выполняться для связных графов. Мы также рассмотрим интересный пример того, что два графа с изоморфными группами автоморфизмов могут не обязательно иметь одно и то же число фиксации. Кроме того, мы изучаем границы для фиксирующих чисел и стратегии определения фиксирующих множеств графа на основе его группы автоморфизмов и набора вершин.

Аули Фишер

Фиксация номеров классов графа

Относительно новая тема в теории графов, фиксация множеств и чисел графа дает новый способ определения симметрии графа и, таким образом, может применяться во многих различных приложениях.Подмножество S вершин графа G называется фиксирующим множеством, если всякий раз, когда g,h в Aut(g) совпадают по вершинам S, они совпадают по всем вершинам G. То есть S является фиксирующим множеством, если всякий раз, когда g и h являются автоморфизмами со свойством g(s) = h(s) для всех s из S, тогда g=h. Фиксирующее число графа G — это наименьшее целое число r, при котором G имеет фиксирующее множество размера r. Сначала мы покажем фиксирующее число различных классов графов. Затем изучите, как применить эти классы и другие свойства для нахождения фиксированного числа произведений графа, в частности декартова произведения.Забегая вперед, мы исследуем возможные применения фиксирующих чисел.

Эбигейл Лиан

Венгерский подход к программе математики средней школы через комбинаторику

Комбинаторика часто исключается из традиционных учебных программ по математике средней школы в США, хотя она соответствует целям различных общих основных государственных стандартов и стандартов NCTM. Он был введен в учебную программу в Венгрии в 1987 году с использованием педагогики, которая позволяет учащимся сотрудничать и бросать вызов друг другу при решении проблем.Основная цель этого исследования состояла в том, чтобы изучить, как комбинаторика может вписаться в текущие учебные программы по математике в США, и оценить эффективность венгерского подхода в математическом образовании. Мы разработали проблемные темы, которые представили старшеклассникам, а затем проанализировали их обучение с помощью методов, включающих классификацию распространенных ошибок. Мы используем наши выводы, чтобы определить области дальнейших исследований.

Кори Мелтон

Трехмерная модель деформации глаза с использованием пружинно-массовой сетки

Тупая травма глаза вызывает долговременное повреждение глаза, которое может даже привести к потере зрения.Во время занятий спортом, таких как гандбол, глаза очень восприимчивы к травмам, возникающим в результате тупой травмы. Недавнее исследование, проведенное в компании Pacific, показало, что традиционные защитные очки, используемые гандболистами, не предотвращают травмы глаз от ударов. Методы математического моделирования можно использовать для исследования влияния тупой травмы глаза на глаза. Глаза представляют собой упругие твердые тела, деформацию которых можно смоделировать с помощью дифференциальных уравнений в частных производных. Однако моделирование системы таким образом требует больших вычислительных ресурсов.Таким образом, можно использовать альтернативную систему сетки масса-пружина для упрощения расчетов до связанной системы обыкновенных дифференциальных уравнений. Предыдущий студент из Pacific разработал двухмерную модель сетки масса-пружина для измерения деформации глаза после воздействия различных гипотетических сил. Моя работа расширяет эту модель до трех измерений с тетраэдрической сеткой точечных масс, соединенных пружинами. Наша модель будет использоваться в будущих проектах для тестирования и рекомендации изменений конструкции защитных очков в спорте.

2017

Эмили Бэрри

Методы рейтинга голосования и подсчет Борда

Как группа должна сделать один выбор из более чем двух вариантов? Есть много способов сделать это, и теория социального выбора посвящена математическому и логическому исследованию этих методов. Одним из таких методов является счет Борда, так называемый «ранговый метод». Счетчик Борда используется, например, для ранжирования команд колледжей. В недавней статье исследовано непрерывное среднее всех ранговых методов.Авторы доказали, что это среднее эквивалентно графу Борда. Однако использование непрерывного среднего включает необоснованные ранговые методы. В этом докладе мы рассмотрим более разумное дискретное среднее и покажем, что это среднее также эквивалентно счету Борда.

Эван Карлсон

Динамика электромагнитно-индуцированной прозрачности

На границе между областями физики и информатики лежит область квантовых вычислений. Цель квантовых вычислений — использовать свет вместо электронов для передачи, интерпретации и хранения информации.Центральным вопросом в этой области является память. В настоящее время существует несколько возможных методов хранения света в качестве памяти для квантового компьютера. Одним из потенциальных кандидатов на роль оптической памяти является квантовое явление, известное как электромагнитно-индуцированная прозрачность (ЭИП). Во время EIT окно передачи индуцируется на непрозрачный атомный резонанс. Свет, настроенный на это окно передачи, испытывает резкое снижение групповой скорости, что приводит к измеримой задержке световых импульсов. Оптические свойства среды определяются системой из трех связанных линейных дифференциальных уравнений. Мы стремимся как численно, так и аналитически решить эти уравнения, чтобы охарактеризовать оптические свойства среды и исследовать оптимальные условия для EIT.

Прескотт Девинни

Системно-динамическая модель шистосомоза: сравнение целостных вмешательств с частичными

Мы используем модель системной динамики для анализа относительных затрат и преимуществ целостного и разрозненного подхода к снижению заболеваемости шистосомозом. Мы развиваем глубокое понимание математики, лежащей в основе системной динамики, а также ее приложений в математической эпидемиологии.Наше использование этого метода для шистосомоза является новым, хотя он имеет ограниченное применение в эпидемиологии и общественном здравоохранении. Последствия для эпидемиологии и математики заключаются в том, что системная динамика может быть подходящей техникой для быстрого и интуитивного моделирования системы, и она особенно эффективна при передаче сложных идей нетехнической аудитории.

Тайла Куйл

Математическое моделирование парасимпатического влияния на клетки желудочков

Мы разработали систему дифференциальных уравнений, которая моделирует потенциал действия клеток желудочков, когда парасимпатический нейротрансмиттер ацетилхолин высвобождается в синоатриальный узел через правый блуждающий нерв. Эта модель основана на модели, разработанной Beeler-Reuter, и связана с моделью синоатриального узла Демира, Кларка и Джайлса. Изучаются эффекты парасимпатической стимуляции на стимуляцию сердца и исследуются упрощенные версии этой модели.

Чарльз Морс

Кристаллическая структура

Кристаллография — это изучение кристаллов и их структуры. Такое понимание внутренней структуры кристаллов важно в химии и физике твердого тела.Я хочу взять современное математическое понимание кристаллов и того, как они структурированы, и применить его к еще не открытым кристаллам. Я искал комбинации двух элементов, не встречающихся вместе в природе, и, изучая кристаллографию, делаю предсказания относительно структуры теоретических кристаллов и их различных свойств.

Виктория Правитц

Стремление к справедливости: анализ Settlers of Catan

 Поселенцы Катана – это популярная стратегическая настольная игра, в которой из-за случайной расстановки доски и использования игральных костей используется вероятность. Часто игра начинается неравномерно для игроков, при этом первый игрок получает вероятностное преимущество. Справедливое деление — это активная область математики, которая решает проблему разделения набора ресурсов между несколькими людьми. Мы изучаем несколько алгоритмов справедливого деления, применяем алгоритм «Последний убавитель» к настройке Settlers of Catan и исследуем последствия.

Джейкоб Ричардс

Моделирование влияния кардиальных кавеол на потенциал действия в клетке синоатриального узла.

Мы разработали математическую модель сердечного потенциала действия в клетках синоатриального узла, которая включает влияние сердечных кавеол Эффекты кавеол можно моделировать с помощью функций плотности вероятности. Эти функции плотности вероятности позволяют нам моделировать случайность открытия и закрытия тысяч кавеол, образующихся вокруг клетки. Наконец, эти результаты сравниваются с результатами предыдущего исследования математического моделирования стохастических кавеол в клетках сердца.

Брендон Уолтерс

Множество масок матроидов

По сравнению со многими математическими предметами, матроиды относительно новы, они были обнаружены только в середине 1900-х годов. Однако матроиды — очень гибкий предмет, поскольку они появляются в нескольких, казалось бы, несвязанных математических областях, включая линейную алгебру, конечные геометрии, латинские квадраты и теорию графов. В этой презентации будут рассмотрены свойства матроидов, некоторые области математики, в которых они применяются, некоторые интересные результаты, полученные в результате их открытия, и то, что эти результаты могут рассказать нам о том, как пересекаются различные области исследований.

Дэниел Йейтс

Картины дифракции света для применения в телескопе

Современные оптические телескопы дают нам беспрецедентные изображения Вселенной, позволяющие исследовать природу темной материи и темной энергии. Для больших оптических телескопов требуются сложные оптические системы, часто включающие несколько линз и зеркал. Картины дифракции света в фокальных плоскостях влияют на разрешение изображения, поэтому для обеспечения высокой точности изображения требуется хорошее понимание дифракции.В этом проекте рассматриваются элементы дифракции, такие как принцип Гюйгенса-Френеля и функция рассеяния точки, чтобы понять, как они влияют на оптику телескопа. Кроме того, в этом проекте сравниваются различные теории дифракции, в том числе дифракция Кирхгофа, Фраунгофера и дифракции Френеля, чтобы определить сходства и различия между теориями дифракции.

2016

Джереми Тейт Кэмпбелл

Математическая оптимизация и проблема эвакуации

Исследование операций (OR) — это область математики, в основе которой лежит идея абстрагирования основных элементов проблемы и их анализа для получения оптимального решения для реализации.Конкретной ветвью OR, которую мы изучали, была математическая оптимизация, процесс максимизации или минимизации реальной функции с учетом набора ограничений. Активной областью исследований в области прикладной математики является применение теории для моделирования эвакуации из зданий. Их моделируют, объединяя физические местоположения в сеть узлов и дуг и используя линейное программирование, чтобы найти оптимальное решение для эвакуации. Мы применили это ко второму этажу Price Hall, где с помощью линейного программирования обнаружили, что время эвакуации и вместимость здания имеют несколько линейную зависимость.

Дэвид Карр

Актуарная модель долга по студенческой ссуде

По мере того, как средняя задолженность перед колледжем увеличивалась, количество дефолтов быстро росло. В этой презентации мы разрабатываем математическую модель, которая поможет нам изучить влияние роста числа дефолтов на финансовые учреждения. Мы рассматриваем несколько факторов, связанных с ростом уровня дефолтов.

Бриджит Дейли

Использование и неправильное использование регрессии для химического анализа

Стандартной практикой в ​​аналитической химии является использование линейной регрессии, особенно для калибровки аналитических приборов. Если бы для оценки выхода прибора для известной концентрации аналита использовалась линия регрессии, все было бы в порядке. Однако химики используют эту линию в обратном порядке, оценивая концентрацию неизвестного аналита на выходе прибора. В этом докладе мы рассмотрим, как неправильное использование линии регрессии влияет на оценку концентрации.

Эмили Гауб

Одна ладья, две ладьи, красная ладья, синяя ладья: исследование полиномов ладей разных цветов

Ладейные многочлены тесно связаны с расстановкой ладей в шахматной игре.Сначала рассмотрим шахматную доску размерами m на n. Ладьи размещаются на доске таким образом, что они не атакуют, то есть никакие две ладьи не находятся в одном ряду или столбце. Тогда в реальной игре в шахматы эти ладьи не могли атаковать друг друга. Ладейный многочлен — это производящая функция, в которой коэффициенты члена степени r дают количество расстановок r неатакующих ладей на данной доске. Это стандартный способ проверки ладейных многочленов.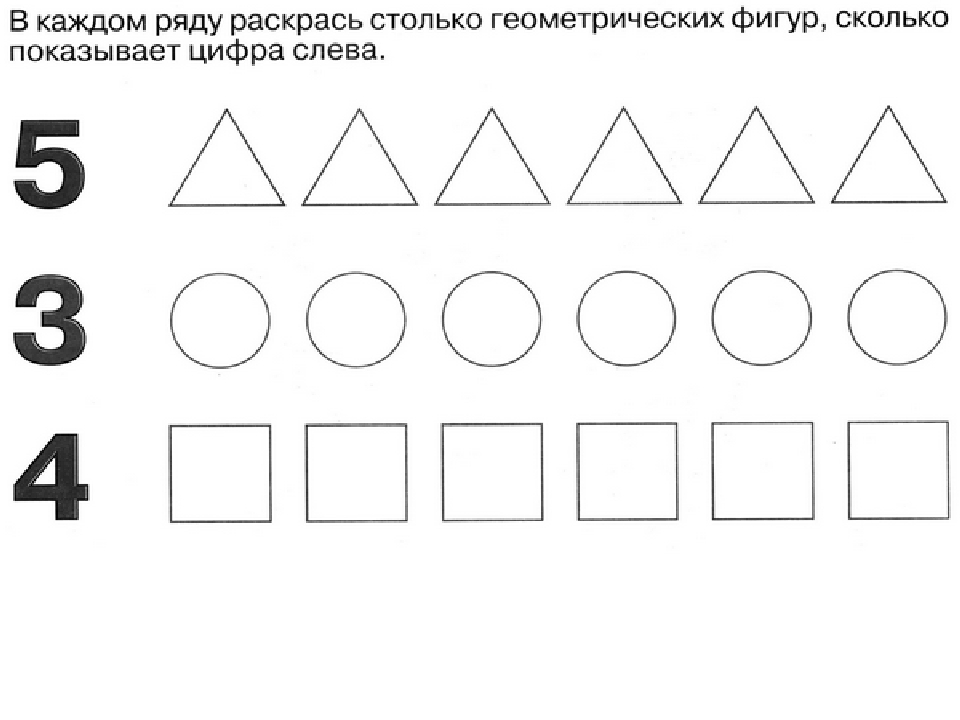 Для моего первоначального исследования я рассматриваю случай, когда ладьи отчетливо окрашены.В частности, существует набор ладей двух цветов, где ладьи одного цвета могут находиться в одном ряду или столбце и не считаться атакующими. Ладьи атакуют только тогда, когда они делят ряд или столбец с ладьями другого цвета. Результаты включают максимальное количество четко окрашенных ладей, которые могут быть размещены на данной доске, количество расстановок ладей, выражение этих значений в виде многочлена и выражение полиномов ладей в виде графиков.

Эшли Гроган

Год

Антонио Гауди — один из самых известных архитекторов в истории.Его влияние в Барселоне, Испания, стало культовым благодаря различным произведениям, таким как Саграда Фамилия и Палау Гуэль. Различные арки внутри этих зданий оставляют туристов в недоумении, но их значение заключается не только в определении их визуальной красоты. Из различных изображений его арок мы можем построить наборы данных и построить графики, чтобы проанализировать лежащие в их основе математические структуры.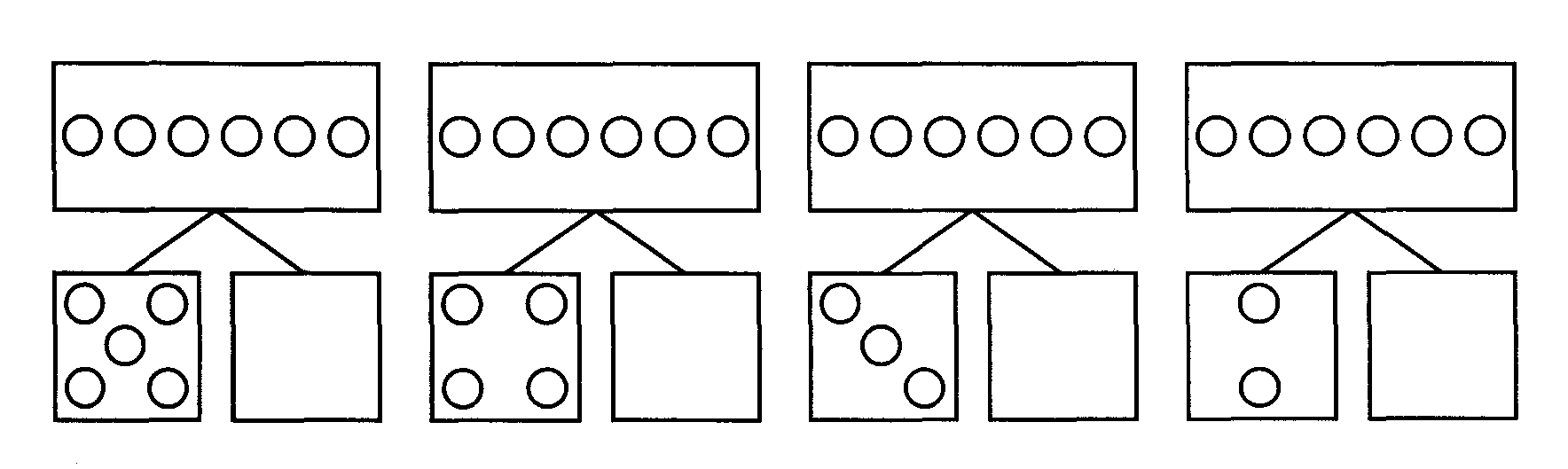 После получения уравнения контактной сети из принципов оптимизации мы используем метод наименьших квадратов, чтобы найти контактную сеть, наиболее подходящую для кривой каждой арки.Контактная сеть — это часть катеноида: поверхность, минимизирующая общую площадь в евклидовом пространстве. Мы обнаруживаем, что некоторые из арок Гауди тесно связаны с параболами, и, что удивительно, мы обнаруживаем арку, которая лучше подходит для гибрида функций параболы и контактной сети. Использование математики для создания этих проектов привело к структурному и визуальному одобрению со стороны гостей, дизайнеров и многих начинающих архитекторов.

Ханна Герберт

Моделирование деформации глаза

Моделирование оболочек и различных органов тела может быть полезно для прогнозирования степени повреждений от сильных ударов.В частности, глаза особенно уязвимы для потенциальных ударных травм в таких видах спорта, как гандбол. Точная формулировка модели для глаза позволила бы провести доступные испытания и разработать более эффективную защиту очков. Поскольку глаза являются примерами упругих твердых тел, их деформация под действием сил может быть охарактеризована системами дифференциальных уравнений в частных производных. Однако поиск решений таких сложных задач чаще всего требует больших вычислительных ресурсов. Таким образом, можно применить альтернативный подход, такой как система масса-пружина.Модель масса-пружина сводит задачу к большой системе связанных обыкновенных дифференциальных уравнений, которые мы используем в нашей модели. В основе нашей модели лежит модель Сатьянараянана и его коллег, за исключением того, что мы использовали другую конфигурацию пружинной сетки для упрощения расчетов. Мы реализуем дискретизацию нашей модели, используя несколько численных методов для анализа повреждения глаза в нескольких гипотетических сценариях воздействия.

Мариса Хаффман

Детектор признаков SURF и дескриптор

Компьютерное зрение состоит из методов обработки и анализа изображений для получения числовой информации. В области обнаружения и распознавания предметов произошли недавние достижения, такие как разработка алгоритма Speeded Up Robust Features (SURF).

Ян Кит Николас

Раскраска графика с меньшим количеством цветов, чем хроматический номер

Мы определяем тип правильной раскраски графа, который использует количество цветов, меньшее или равное хроматическому числу. Правильная раскраска графа относится к присвоению меток вершинам графа таким образом, чтобы смежные вершины имели разные метки.Эта правильная раскраска графа, называемая разноцветной, возникает из естественного способа комбинирования цветов с помощью комбинаций, мало чем отличающегося от комбинирования цветов краски. Разноцветие присваивает наборы цветовых комбинаций каждой вершине таким образом, что наборы полностью не пересекаются для соседних вершин. В свою очередь, мы также вводим более слабую версию разноцветной раскраски, называемую слабой разноцветной раскраской, которая ослабляет условие полной непересекаемости. Подобно хроматическому числу, графы имеют число разноцветного (и слабого разноцветного числа), которое обозначает минимальное количество цветов, необходимых для разноцветного (и слабого разноцветного) графа.Найдены необходимые и достаточные условия, при которых число разноцветности и число слабой разноцветности является не более чем хроматическим числом для любого (простого) графа.

Эсбейда Рамос

Цвета и продукты, и графики, о боже!

Раскраска графа — это тип маркировки графа, при котором вершины раскрашиваются таким образом, чтобы никакие две соседние вершины не были одного цвета. Наименьшее количество цветов, необходимое для раскрашивания данного графа, называется хроматическим числом. Есть несколько способов объединить два графика, взяв их произведение; мы сосредоточимся на тензорном произведении или прямом произведении.Мы исследуем свойства прямого произведения и некоторые способы определения границ хроматического числа. Эти идеи ведут нас в мир вопросов без ответов. Недоказанный, но широко принятый ответ на один из этих вопросов известен как гипотеза Хедетниеми и была впервые выдвинута Стивеном Т. Хедетниеми в 1966 году. Его гипотеза служит для демонстрации того, что никакое тензорное или прямое произведение нельзя раскрасить неожиданно малым числом цветов. . Кроме того, мы также спрашиваем, что происходит, когда не хватает доступных цветов? Чтобы ответить на этот вопрос, мы используем подход, называемый многоцветием, который использует набор цветов графика для создания дополнительных цветовых вариантов.Наши результаты находят способ исследовать произведения задач многоцветия, а также способы вычисления хроматического числа прямого произведения.

Кристалл Зусбауэр

Произведения графов и раскраски в связи с гипотезой Хедетниеми

В теории графов определено много типов операций произведения. Эти продукты используют вершины и ребра двух (не обязательно разных) графов для создания нового графа. Мы сосредоточимся на четырех важных типах произведений графов: декартовом произведении, прямом произведении, сильном произведении и лексикографическом произведении. Кроме того, мы изучаем способы маркировки графов с помощью раскраски графов и списков, а также исследуем хроматическое число графа. Наконец, мы связываем обе темы друг с другом, исследуя гипотезу Хедетниеми и выясняя, какая работа была проделана, чтобы попытаться доказать или опровергнуть эту гипотезу.

Эмма Винкель

Пи: его история, свойства и введение в класс средней школы

В этой презентации мы исследуем математическую константу пи в различных контекстах.Мы обсудим историю использования числа пи, доказательства некоторых из наиболее важных свойств числа числа и необходимое концептуальное понимание числа числа в образовательной среде.

Вубин Чжан

Комбинаторная теория игр

Проиграть в игре может быть намного сложнее, чем выиграть. В комбинаторной теории игр попытка выиграть называется «нормальной игрой», а попытка проиграть — «жалкой игрой». Теория нормальной игры была хорошо изучена к 1950-м годам, в то время как потребовалось еще пятьдесят лет, чтобы продвинуться вперед в теории мизерной игры. Мы исследуем новые методы, разработанные для изучения игры со страданием, и используем их для решения жалкой версии игры Кейлс.

Блейк Энтони

Квантовая государственная томография

Скорость передачи данных в электронике достигает своего максимума, что вызывает переход к использованию света для передачи информации в таких технологиях, как компьютеры и телевизоры. Целью моего проекта была разработка методики определения частот, присутствующих в свете.Метод хранения информации в свете состоит в том, чтобы послать ее через газ, такой как рубидий. Чтобы понять влияние газа рубидия на информацию, содержащуюся в свете, мы смоделировали свет, проходящий через газ, используя уравнения Максвелла. Затем мы использовали массив детекторов света, чтобы построить график интенсивности двух световых лучей, падающих на детекторы под углом 12 мрад. Первый луч был лучом высокой интенсивности с одной частотной модой, тогда как другой луч был лучом низкой интенсивности, состоящим из нескольких частотных мод. Из интерференции двух лучей мы извлекли частотные моды, присутствующие с помощью дискретного преобразования Фурье, чтобы увидеть, как газ влияет на частоты.

Стефани Картер

Нелинейная модель для комбинированной радиофармацевтической терапии

Это расширение линейной модели комбинированной радиофармацевтической терапии нейроэндокринных опухолей с использованием 131I-метайодбензилгуанидина и 90Y-DOTA-D-Phe1-Tyr3-октреотида. Как и исходная линейная модель, эта модель пытается оптимизировать количество радиации, доставляемой к опухоли, без превышения критической дозы, поглощаемой другими органами.Однако в этой нелинейной модели мы моделируем эффекты не одного, а двух видов комбинированной радиофармацевтической терапии. Второе лечение основано на количестве каждого радиофармпрепарата, использованного при первом лечении, и диаметре опухоли до и после доставки излучения. Результатом является задача оптимизации с четырьмя переменными, которая предоставит дополнительную информацию и варианты лечения, которые линейная модель не могла предсказать.

Спенсер Чендлер

Паттерны в треугольнике (a,b)-Паскаля по простому модулю

Последовательность Фибоначчи, важная последовательность целых чисел, генерируется с помощью рекурсии F _n =F _n-1 +F _n-2 .Хорошо известно, что последовательность Фибоначчи можно найти в виде суммы обратных диагональных чисел в треугольнике Паскаля. В этом докладе мы рассмотрим обобщение чисел Фибоначчи, называемое (a,b)-числами Фибоначчи. Мы строим модифицированный треугольник Паскаля, в котором можно найти (a,b)-числа Фибоначчи, и исследуем закономерности в этом треугольнике по простому модулю.

Джули Давенпорт

Радионуклидная терапия: оптимизация режима дозирования

В этой статье мы предлагаем математическую модель, которая минимизирует размер опухоли после двух обработок радионуклидами.В этом исследовании мы покажем, что способ лечения нейроэндокринной опухоли с помощью двухкомпонентной терапии состоит в том, чтобы дать вторую дозу как часть максимальной дозы до того, как опухоль восстановится после эффекта первой дозы. Количество этой второй дозы определяется индивидуальными параметрами пациента и скоростью восстановления пораженных критических органов. В нашем методе используется программное обеспечение для математических вычислений для оптимизации эффекта терапии. Наши результаты дают оптимальный график двух лечебных процедур.

Брэндон Хармс

Многомодовое измерение квантового состояния

В нашем нынешнем электронном мире мы обнаружили необходимость стремиться к более высоким скоростям. Одним из способов решения этой задачи является передача информации с помощью световой фотоники. Чтобы продвигать эту технологию, необходимо иметь возможность охарактеризовать свет, который был остановлен и сохранен. В моем проекте мы смогли охарактеризовать исходный слабый сигнальный луч света, интерферируя его с сильным эталонным лучом и наблюдая картину интенсивности, сформированную в пространстве на нашем матричном детекторе.Мы определяем пространственные частоты или «моды», связанные с этой интерференционной картиной, используя анализ Фурье. С помощью нашего метода обнаружения массива мы можем построить график зависимости среднего количества фотонов от угла моды плоской волны для каждой моды, которая вносит свой вклад в картину.

Виктор Рилли

Дифференциальные уравнения

Мы представляем несколько элементарных и общих методов решения линейных и нелинейных дифференциальных уравнений первого порядка, которые удовлетворяют определенной форме. Анализ предназначен скорее для того, чтобы дать читателю идеи, чем для того, чтобы представить полную и всеохватывающую теорию дифференциальных уравнений, которые мы изучаем.Тем не менее, мы представляем очень общие тесты, которые можно провести над рассматриваемыми дифференциальными уравнениями. Если уравнения удовлетворяют тестам, решения дифференциальных уравнений можно выписать напрямую. Анализ может быть распространен на большой класс дифференциальных уравнений и уже может касаться общего линейного дифференциального уравнения первого порядка, уравнения Бернулли, разделимых дифференциальных уравнений и нескольких дифференциальных уравнений, которые мы, возможно, решим первыми. Мы заканчиваем статью распространением на дифференциальные уравнения более высокого порядка и обсуждением общности методов.

Тема внешнего бильярда — относительно новая область геометрии, многие результаты которой ждут своего открытия. В самом широком смысле внешний бильярд можно рассматривать как грубую модель того, как объекты будут вращаться вокруг тела. Обычно возникают два общих вопроса об орбитах: какие орбиты в конечном итоге будут повторяться или быть периодическими, а какие орбиты в конечном итоге станут неограниченными, удаляясь все дальше и дальше от тела.Мы сосредоточимся на том, какие орбиты в гиперболическом пространстве будут периодическими. Мы определяем особый тип орбиты, называемый специальной орбитой. Показано, что если выпуклый многоугольник имеет особую орбиту, то все его орбиты являются периодическими.

Трехмерные модели объектов реального мира можно получить с помощью методов сканирования различной стоимости и качества. В этом исследовании мы воспроизвели самый дешевый из таких методов: сканирование структурированным светом.Мы улучшаем ранее существовавшие методы, вычисляя ошибку как в модели, так и в самой модели, а затем используя эту ошибку, чтобы определить, где выполнять дальнейшее сканирование.

Линейное программирование было широко признано одним из наиболее важных научных достижений середины 20-го века. Эта замечательная область математики породила инструменты, ставшие отраслевым стандартом в области исследования операций.Эти инструменты применимы к широкому классу проблем принятия решений, относящихся почти ко всем отраслям. Наиболее распространенный тип приложения включает в себя общую проблему распределения ограниченных ресурсов между конкурирующими действиями наилучшим (то есть оптимальным) способом. В нашем исследовании рассматривается математическая теория линейного программирования, а также множество форм, которые могут принимать эти задачи. Логика и методы решения таких задач оптимизации затем обсуждаются в контексте приложений к бизнесу и производству.

Диофантовы уравнения, в которых интерес представляют только целочисленные решения, изучаются с 3 ^-го -го века. Также большой интерес представляют диофантовы неравенства. Действительно, это неравенство возникало даже в старших завершающих проектах. В 2013 году Эван Купер столкнулся с диофантовым неравенством в своей работе по улучшению рейтинговой системы студенческого футбола.Куперу нужно было найти так называемые минимальные решения своего неравенства. Вдохновленные его работой, мы пытаемся определить количество минимальных решений общего линейного диофантова неравенства. Мы начнем с исследования случая двумерного линейного диофантова неравенства и найдем простое замкнутое выражение для числа минимальных решений.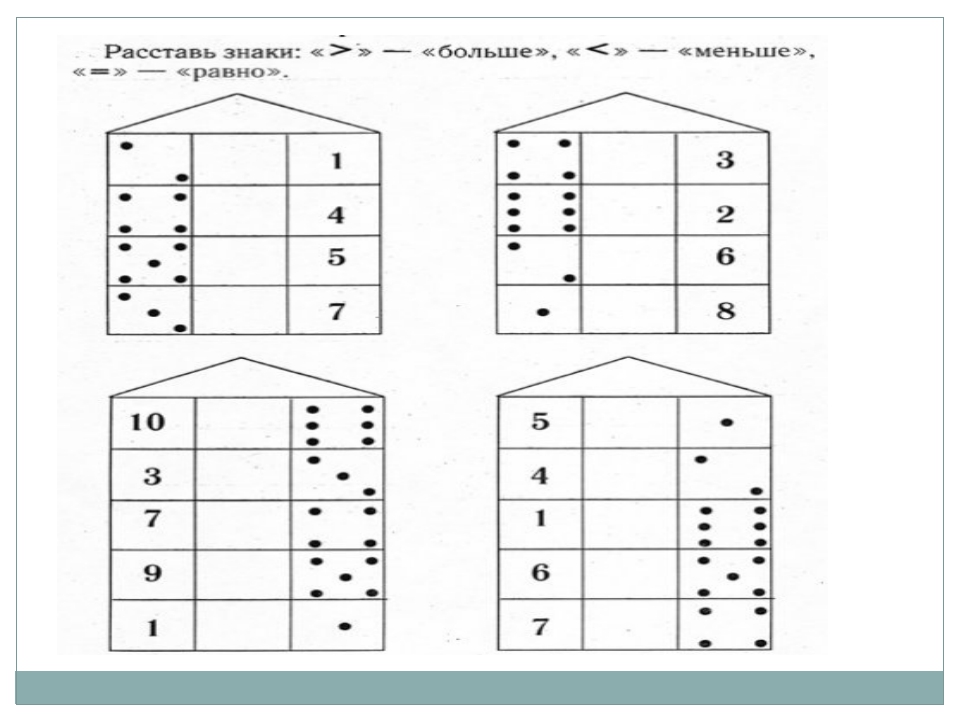 Для задач более высокой размерности мы можем определить рекурсивную формулу для числа минимальных решений. Наконец, мы используем полиномы Эрхарта, чтобы найти замкнутую форму как для верхней, так и для нижней границы числа минимальных решений общего линейного диофантова неравенства от n переменных.

Традиционные 3D-дисплеи создают иллюзию глубины, предоставляя отдельные изображения для обоих глаз, однако в настоящее время не существует способа получения изображений с правильным фокусным расстоянием. Для фокусировки света требуется, чтобы лучи собирались вместе под правильными углами, создавая сходящийся волновой фронт: волновой фронт с кривизной. В этом проекте мы исследуем использование массивов линз для добавления кривизны волновому фронту, создаваемому обычным экраном дисплея.Мы показываем, что, выбирая правильные пиксели, можно заставить лучи сходиться в точке перед экраном.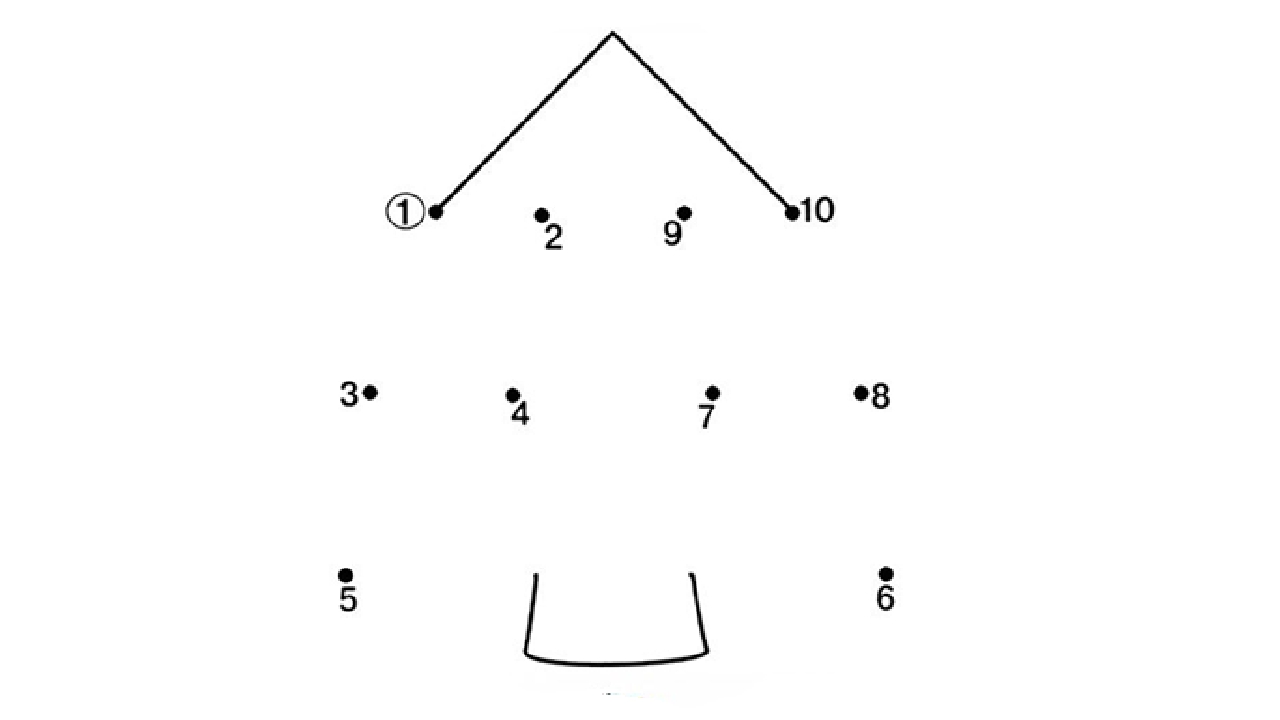 Выведена векторная версия закона Снелла, которая используется для предсказания угла, под которым свет от произвольного пикселя выйдет из системы линза-экран. Полученная карта «пиксель-угол» облегчит разработку будущего контента для систем отображения на основе линз.

Две модели (основанные на модели желудочка морской свинки Luo-Rudy 1) были созданы для анализа эффектов кавеолярного натриевого тока на один потенциал сердечного действия и одномерного распространения потенциала сердечного действия в линии кардиомиоцитов. .Имеющиеся данные свидетельствуют о том, что открытие кавеол задействует дополнительные натриевые каналы на мембране кардиомиоцитов, которые могут влиять как на выброс пикового напряжения, так и на максимальную скорость восходящего импульса потенциала действия сердца — максимальная скорость восходящего импульса, в свою очередь, может изменить скорость проведения электрического сигнала. Мы рассмотрели два механизма открытия кавеол. Первый механизм открытия имитировал участок мембраны размером 1 см ² , перфузированный агонистом β-адренорецепторов, который открывал определенное количество кавеол на мембране.Второй механизм открытия имитировал участок мембраны размером 1 см ² со стохастически открывающимися кавеолами, которые открываются в соответствии с процессом Пуассона. Влияние этих двух механизмов открытия кавеол на один потенциал действия сердца с использованием модели LR1 сравнивали с предыдущими результатами вычислений с использованием модели желудочка крысы Pandit et al. Наше моделирование (которое включало переменную емкость) выявило увеличение пикового выброса напряжения на 4,1% и увеличение максимальной скорости подъема на 19,1% при увеличении тока натрия на 42% из-за β-адренергической стимуляции.Включая стохастически открывающиеся кавеолы, мы наблюдали задержку реполяризации желудочков, характерную для серьезного сердечного заболевания, называемого синдромом удлиненного интервала QT.

Геометрические разрезы включают в себя разрезание одной или нескольких фигур на части, которые можно переставлять, чтобы сформировать другие фигуры. Вскрытие можно использовать для предоставления визуальных доказательств математических тождеств, таких как теорема Пифагора, и для выявления ранее неизвестных тождеств.Они могут помочь тем, кто не знаком с высшей математикой, понять некоторые фундаментальные результаты. В этой презентации мы представляем метод рассечения и иллюстрируем несколько интересных примеров. Наконец, мы обсудим теорему Уоллеса-Бойяи-Гервина, которая лежит в основе метода рассечения.

На пересечении математики и информатики лежит теория графов.Графы состоят из вершин или узлов и ребер, которые соединяют вершины. Общие приложения включают сетевые модели и компьютерные алгоритмы, а теория графов предлагает решения и понимание многих практических проблем. Относительно новая область теории графов, графы и последовательности де Брейна изначально «решали проблему поиска двоичной строки минимальной длины, которая содержит в качестве (непрерывной) подстроки каждую двоичную строку заданной длины-k». Эти графы имеют длину k битов как вершины, состоящие из n-буквенного алфавита.Сдвиги символов указывают направление движения от одной вершины к другой. Уникальные характеристики делают их хорошими кандидатами для моделирования одноранговых компьютерных сетей. Представлены свойства, характеристики и приложения графов де Брёйна и им подобных.

Геометрическая теория групп связывает алгебраические объекты с геометрическими объектами и дает возможность использовать геометрию для изучения алгебры. Для заданной конечно представленной алгебраической группы можно определить ее граф Кэли и изучить геометрические свойства этого графа. Некоторые вершины графа Кэли называются тупиками, а соответствующие элементы в ассоциированной группе важны с алгебраической точки зрения. Мы исследуем тупики в конечных группах фонарщиков, классифицируем эти элементы по отношению к естественному порождающему множеству группы. Мы также исследуем отношение числа тупиковых элементов к порядку группы.

Чисел и слов иногда не хватает при решении конкретных задач в области математики и информатики.Например, предположим, что мы хотим представить набор компьютеров и соединений между ними. Мы могли бы начать описывать их словами, но вместо этого мы кладем карандаш на бумагу и рисуем точки (точки, конечно, являются галактическим стандартом для представления случайных объектов), чтобы представить компьютеры, и линии, соединяющие точки, чтобы представить связи. Теперь у нас есть четкое представление о том, что происходит с тем, что мы называем графом! Теперь предположим, что мы столкнулись с проблемой поиска пути через этот граф, который проходит через каждую точку и возвращается к первой точке, с которой мы начали. Что, если мы усложним граф, заставив связи иметь направления? Возникает логичный вопрос: как лучше подключить эти компьютеры, чтобы обеспечить более высокую скорость подключения? Что, если у нас нехватка кабеля и нам нужно подключить максимальное количество компьютеров, не слишком жертвуя возможностью подключения? Эти ситуации и графики Мура моделируют графы Каутца и Де Брейна. Эти два графа используются для структурирования сетей, таких как архитектуры параллельных вычислений и одноранговые сети, потому что они очень близки к границе Мура.Это означает, что граф имеет высокую связность в сети в дополнение к гарантии максимального расстояния, которое должно пройти сообщение, прежде чем оно достигнет пункта назначения. Граф Каутца в этом отношении лучше, чем граф Де Брейна. С другой стороны, первоначальный источник вдохновения для графа де Брейна, последовательность де Брейна, показывает, что в этих графиках происходит нечто большее, чем кажется. Мы строим эти графы, показываем, на какие вопросы они могут ответить, и связываем воедино концепции последовательностей, ожерелий и графов Мура.

2013

Эван Купер

Рейтинговые системы студенческого футбола: усовершенствования двух моделей

На протяжении многих лет серия Bowl Championship Series подвергалась широкой критике. Многие болельщики считали, что их команды плохо представлены в рейтингах и поэтому не участвуют в более престижных играх постсезонья. В результате этого недовольства NCAA меняет способ определения национального чемпиона в первом дивизионе американского футбола. Начиная с сезона 2013/14, чемпион страны станет победителем двухраундового плей-офф из четырех команд.Экспертный комитет, предположительно по рейтинговой системе, выберет команды для участия в плей-офф. В этом докладе мы исследуем две существующие математические модели, которые можно использовать для ранжирования футбольных команд колледжей. Мы обсуждаем методы, повышающие точность этих моделей, включая использование диофантовых уравнений для взвешивания маржи победы и использование регрессии наименьших квадратов для определения параметров, участвующих в прогнозировании маржи победы в игре.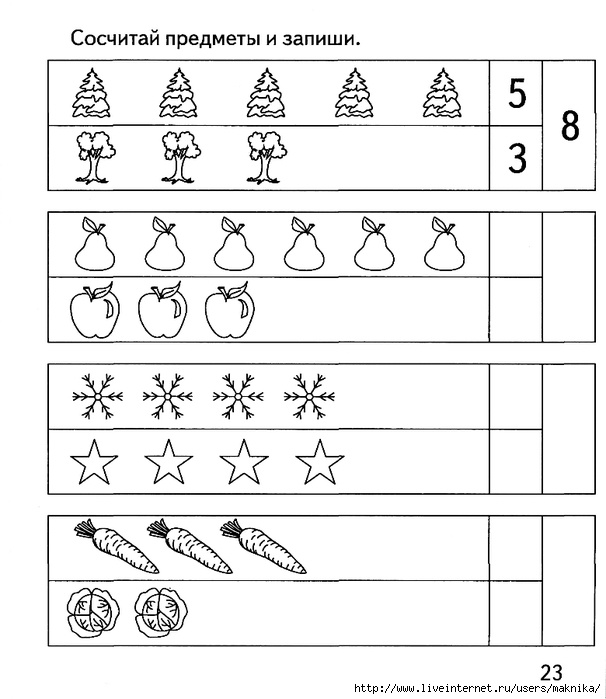

Бриана Флорес

Прогнозирование цунами: линейное или линейноеНелинейные модели

Размышление о цунами, таких как цунами Тохоку в марте 2011 года или цунами на Суматре в декабре 2004 года, напоминает каждому о том, насколько разрушительным и разрушительным может быть цунами. Математические модели предоставляют различные типы информации о цунами, такие как места, на которые оно повлияет, предполагаемое время прибытия на берег, высота и мощность. Опираясь на результаты своих математических моделей, центры наблюдения за цунами могут определить, какие меры предосторожности должны принимать жители.Модели могут быть либо линейными, которые численно более стабильны и быстрее вычисляются, либо нелинейными, которые, как правило, более точны. Время имеет решающее значение для прогнозирования цунами, поэтому более быстрая модель может спасти жизни. Итак, когда линейные модели дают хорошие приближения к нелинейным моделям? Чтобы изучить эту концепцию, я использую программное обеспечение из Тихоокеанского центра предупреждения о цунами и модель, основанную на уравнениях волн мелководья, для сравнения симуляций.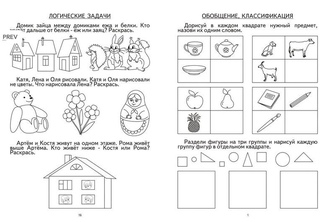

Ханна Ландрус

Сцепки Холдин

Сцепка — это клубок вокруг шеста.При подъеме заминка могла спасти жизнь альпинисту. Во время плавания сцепка могла помешать лодке уплыть. Мы представим модель для определения того, когда сцепка будет удерживаться, и свяжем определитель некоторой матрицы с трением, необходимым для удержания сцепки. Мы рассмотрим последовательности заминок и исследуем минимальное трение, необходимое для удержания зацепок. Это включает в себя изучение последовательности многочленов, коэффициенты которых связаны с треугольником Паскаля.

Кейси Линтон

Математическая неграмотность вызывает финансовый крах: неправильная реализация модели Блэка-Шоулза

Формула Блэка-Шоулза представляет собой математическую модель, используемую для определения стоимости европейского колл-опциона таким образом, который практически исключает риск.После публикации формулы покупки и продажи опционов значительно увеличились. Формула Блэка-Шоулза предполагает идеальные рыночные условия и выводит уравнение в частных производных, обычно называемое конструкцией Блэка-Шоулза; решением УЧП является модель Блэка-Шоулза.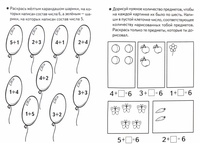 Мы исследуем, что необходимо для того, чтобы модель давала точные результаты, и обнаруживаем, что параметры должны подчиняться нормальному распределению. Считается, что неверные предположения об идеальных условиях на рынке напрямую способствовали краху финансового рынка в 2008 году.Мы пытаемся определить, какие параметры не подчиняются нормальному распределению, и анализируем слабые стороны модели Блэка-Шоулза. В рыночной ситуации 2008 года цена акций следовала распределению с толстым хвостом. Часто по сравнению с нормальным распределением жирные хвосты демонстрируют большой эксцесс, что означает, что наблюдения, далекие от среднего, более вероятны по сравнению с нормально распределенными событиями. Это привело к неправильной реализации модели Блэка-Шоулза и в конечном итоге способствовало краху финансового рынка в 2008 году.

Джек МакКоркель

Разделы азартных игр: подсчет явки электората и подэлектората

Социологи долго пытались объяснить процесс голосования.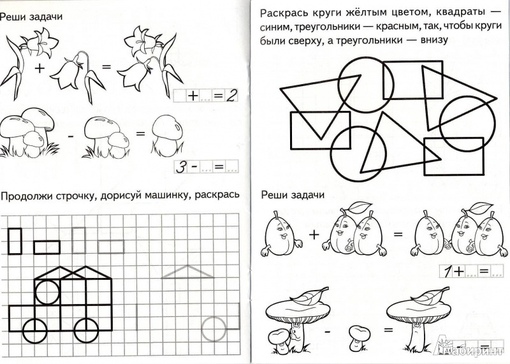 Независимо от используемых статистических методов любая модель голосования становится невероятно сложной, требуя подмоделей, описывающих предпочтения, сопутствующие социально-экономические факторы и важность данного голоса. Я начну с рассмотрения вопросов явки избирателей через призму экономической теории применительно к демократии.Описывая решение голосовать как авантюру, я обращаюсь к эконометрике, чтобы лучше понять явку. Пытаясь согласовать данные с теорией, я также исследую математику включения демографических интересов в явку. Обнаружив, что современным математическим моделям не хватает практичности, надежности и глубины, я предлагаю новую формулировку и исследую способность этой модели предсказывать явку и предпочтения избирателей.

2012

Джесси Амано

Соединение блочных конструкций и матроидов

Блочные конструкции, абстрактные структуры с приложениями для управления экспериментами и сбора данных, во многих случаях показали, что они изоморфны матроидам, другому широкому семейству абстрактных структур. Мы исследуем и обсудим некоторые способы, которыми конкретный класс планов может также описывать матроид, и некоторые способы, которыми определенный тип матроида также может представлять собой план. Мы также рассматриваем случаи, когда существует матроид, но нет плана, и когда существует план, но нет матроида. Поскольку известно, что некоторые алгоритмы создают матроиды или манипулируют ими, они могут быть полезны при построении определенных типов планов. Между тем, тщательное изучение планов может привести к полезным теоремам, применимым к матроидам.

Тони Фернандес

Как ваш треугольник любит плитку

Мы исследуем, какие треугольники могут выкладываться мозаикой на евклидовой или гиперболической плоскости без перекрытия, и точно определяем, какие треугольники укладываются мозаикой без перекрытия. Евклидовы треугольники и гиперболические треугольники имеют разные значения, и это приводит к противоречивым результатам о мозаиках. В частности, хотя евклидов план можно замостить произвольно малыми треугольниками, мы показываем, что существует треугольник наименьшей площади, который замостил гиперболическую плоскость без перекрытия.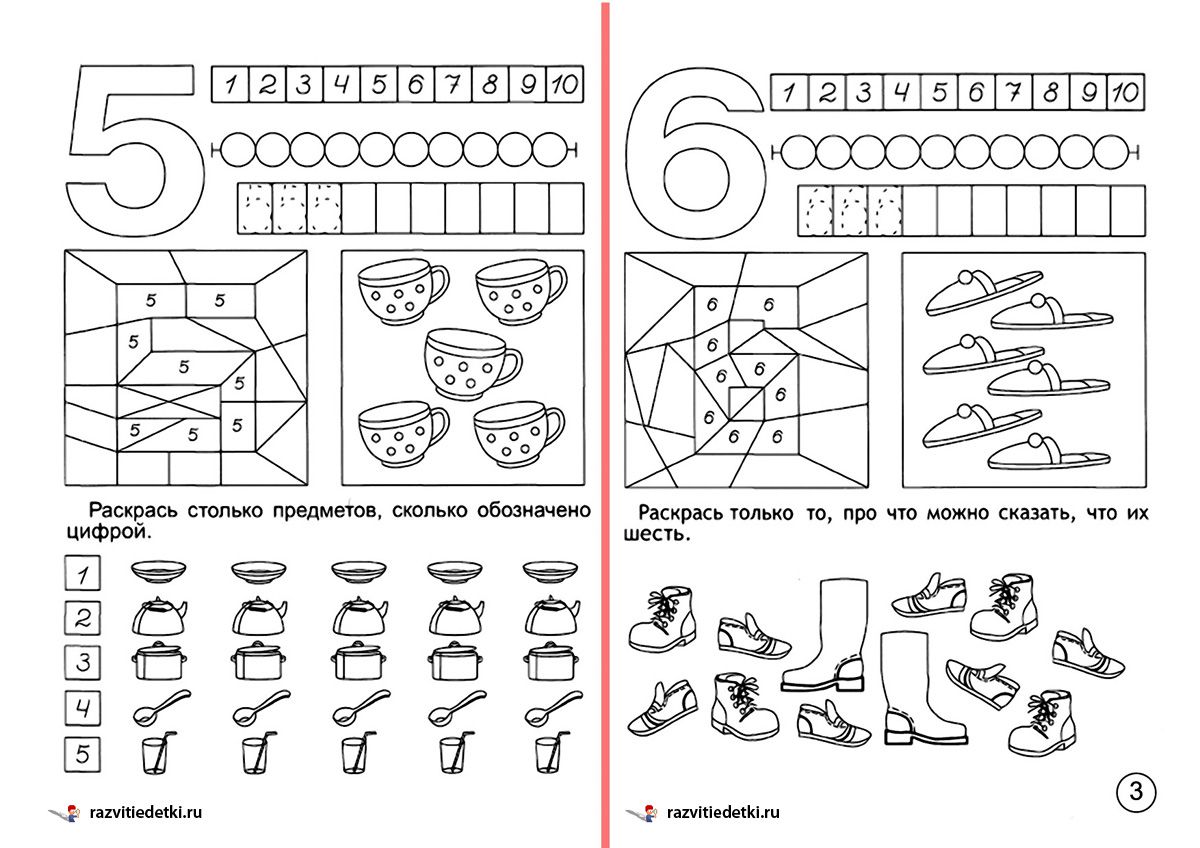

Келли Такамор

США и Австралия: сравнение учебных программ по математике в старших классах

Я сравниваю уровни навыков счета в государственных средних школах Австралии и США, анализируя национальные тесты. В частности, я исследую различия в учебных программах и оценках по математике и соотношу их с такими факторами, как количество выпускников средней школы. Поскольку в Австралии математические темы организованы комплексно, в отличие от принятой в США организации математических тем по предметному содержанию, я сначала оцениваю содержание австралийского национального теста по математике и сопоставляю его с U.S. математические предметы, такие как алгебра I, геометрия, алгебра II и т. д. В частности, я анализирую 9-й класс государственных средних школ штата Орегон, чтобы представлять Соединенные Штаты, и штат Южная Австралия, чтобы представлять Австралию. Я создаю свою собственную шкалу уровней «владения» для австралийских учащихся по предметам и сравниваю данные с уровнями владения языком в США.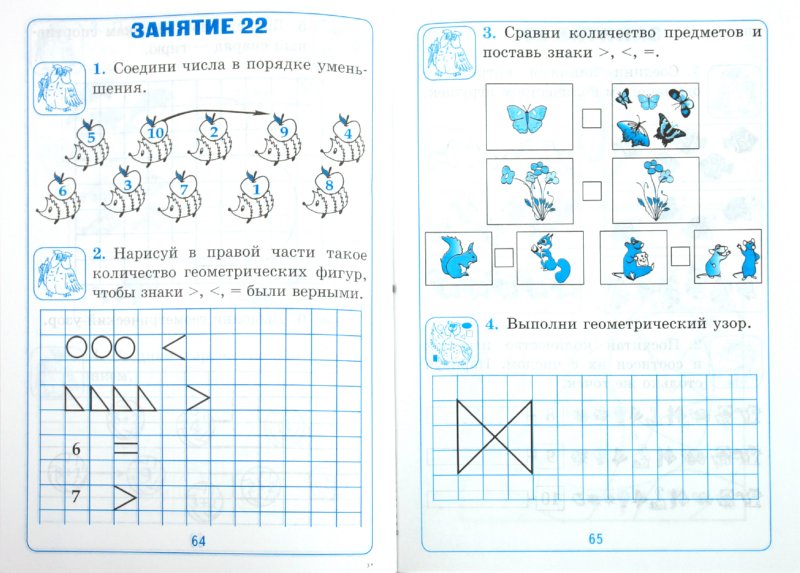 Я использую тесты Австралийской национальной программы оценки грамотности и счета (NAPLAN) и Американскую программу оценки знаний и умений штата Орегон. Тест навыков (OAKS).Затем я статистически анализирую преимущества различных оценок и учебных программ, соотнося результаты с окончанием средней школы, поступлением в колледж на первом курсе и статистикой профессионального мастерства.

Цяньру Ван

Числа Деланнуа: подсчет некоторых ограниченных путей в целочисленной решетке

Числа Деланнуа подсчитывают количество путей в целочисленной решетке из одной точки в другую, где разрешенные ходы должны двигаться на один шаг вверх, на один шаг вправо или на один шаг по диагонали вверх и вправо.В этом проекте мы даем комбинаторные доказательства формул для центральных чисел Делланой и общих чисел Делланой. Мы продолжаем использовать производящие функции, мощный инструмент комбинаторики, чтобы найти другую формулу для общих чисел Деланнуа. Последний процесс обобщается на измерения выше двух.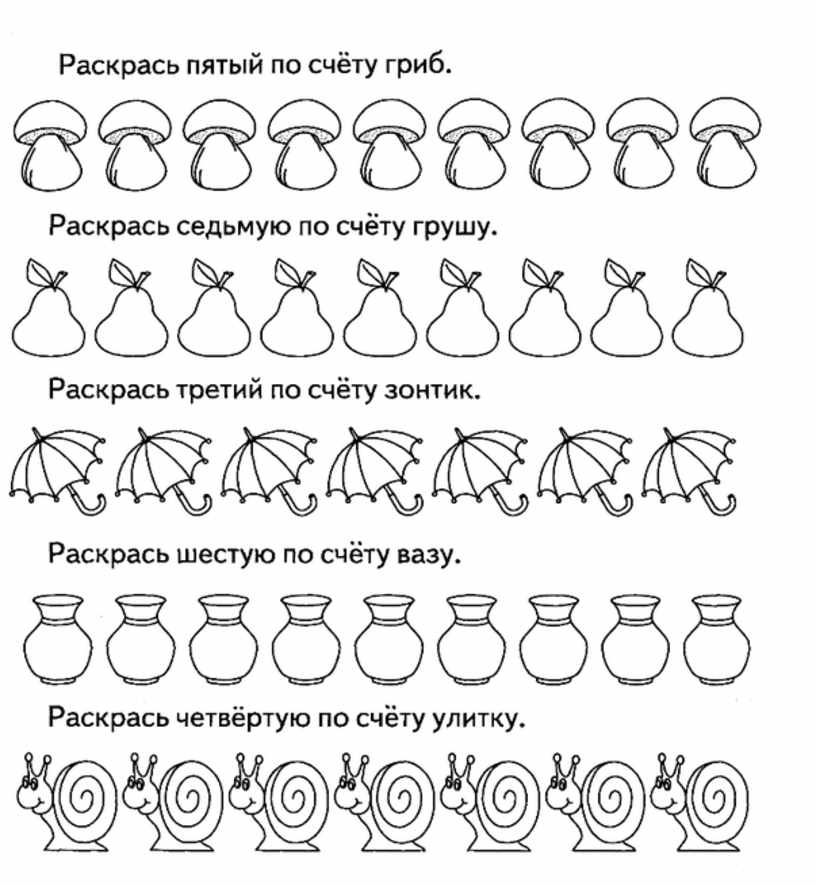 Наконец, мы рассмотрим, что произойдет, если мы добавим дополнительный допустимый ход. Можем ли мы найти формулу теми же методами?

Трэвис Уайт

Математика жонглирования: подсчет последовательностей жонглирования

Может показаться удивительным, что жонглирование и математика связаны.Но многие известные математики также являются опытными жонглерами. На самом деле Рональд Грэм был президентом Международной ассоциации жонглеров и Американского математического общества. Связь может быть связана с тем, что жонглирование — это повторяющееся действие, заложенное шаблонами. Жонглеры описывают эти паттерны с помощью последовательностей. В этом докладе мы узнаем, как классифицировать паттерны жонглирования по количеству жонглируемых мячей, длине паттерна и времени приземления шаров. Кроме того, мы увидим, как зафиксировать график посадки и использовать генерирующие функции для подсчета количества возможных паттернов жонглирования различных периодов.Эти числа иногда появляются в неожиданных местах, и мы исследуем некоторые из таких случаев.

2011

Лана Картер

Игра «Полицейские и грабители»

Игры о вторжении в погоню используются для моделирования или объяснения различных ситуаций из реальной жизни, когда команда казначеев пытается поймать захватчика. Математика, связанная с этими играми, тщательно изучалась на протяжении многих лет, восходя к работам Пьера Бугера, который в 1732 году изучал задачу о пиратском корабле, преследующем убегающее судно.Игры преследования были связаны со многими различными категориями и, таким образом, изучались различными способами и методами. Новаковски представил дискретную версию игры, которая в конечном итоге проложила путь к игре о полицейских и грабителях. Этот проект следует за работой, проделанной Тиной Чжан из Бард-колледжа, которая изучала количество полицейских, необходимое для поимки одного грабителя на конечном графе. Принимая во внимание правила игры, цель этого проекта состоит в том, чтобы вычислить количество копов для различных классов графов и миноров графов, чтобы обобщить теоремы или правила, которые можно использовать для нахождения количества копов, необходимых на определенном графе.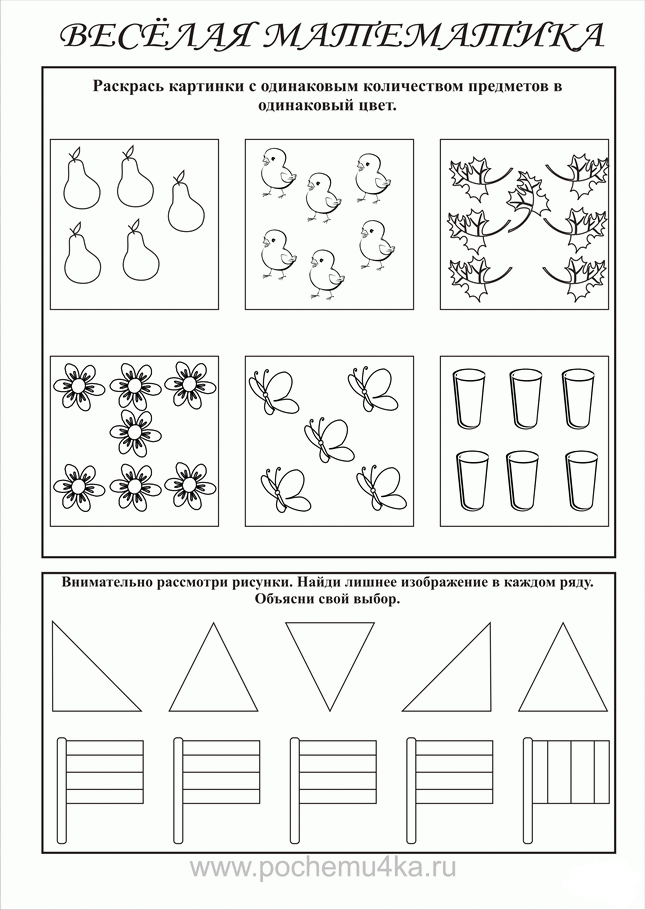

Ребекка Хоффман

Синхронные светлячки

Светлячки в природе ведут себя очень интересно. Когда большие группы светлячков приземляются вместе, светлячки-самцы начинают синхронно мигать, а затем продолжают это поведение. Я изучил математические основы динамических систем, чтобы понять способ моделирования такого поведения. То есть светлячки будут ускорять или замедлять свое моргание, чтобы вспыхнуть вместе с раздражителем. Это поведение можно смоделировать с помощью осциллирующей синусоидальной функции.Я усовершенствовал эту модель, включив в нее треугольную кусочную функцию, чтобы посмотреть, будет ли она лучше моделировать естественное поведение. Кроме того, я использовал Actionscript 3.0, чтобы визуально смоделировать это поведение, чтобы оно соответствовало естественному ритму.

Келси Каку

Полиномиальная интерполяция

Многочлены используются для определения различных функций в таких предметах, как химия, физика, экономика и социальные науки. В реальном мире полином часто подходит для сопоставления с конечным числом точек данных, процесс, известный как полиномиальная интерполяция.Полиномиальная интерполяция в основном практикуется в области действительных чисел. Хорошо известно, что для k точек и x-отличных координат существует единственный многочлен степени k — 1. Однако что произойдет, если мы заменим поле действительных чисел кольцом целых чисел по модулю n? Сохраняются ли существование и единственность, которые мы имели над действительными числами, для кольца целых чисел по модулю n?

Дункан МакГрегор

Поток ренормализационной группы на однородном пространстве

Геометрический поток — это система дифференциальных уравнений, которая искривляет пространство, изменяя его метрику (линейку, по которой измеряется расстояние в пространстве).Поток Риччи — это геометрический поток, который «изгибает» пространство в соответствии с его кривизной, по существу сглаживая его. Этот геометрический поток был использован Перельманом для решения гипотезы Пуанкаре. Поток ренормализационной группы является обобщением потока Риччи, используемого в квантовой теории поля для моделирования изменений метрики, вызванных квантованием классического действия. Мы исследуем существование и единственность решений ФРГ на постоянной кривизне и однородных пространствах.

Дженнифер Новак

Моделирование капиллярных волн

Я смотрю на уравнение, называемое дисперсионным соотношением, которое используется для связи частоты волны со скоростью распространения волны с силами гравитации и капиллярного действия.Сначала я выведу это уравнение, взглянув на «Теорию звука» Рэлея, а затем изменю модель, включив в нее произвольную силу в вертикальном направлении. Применение этого процесса в сельскохозяйственной технике, где мы изучаем размер частиц.

Брэндон Оширо

Что меняется? Проблема максимального расхода

Для данной сети потока с одним источником и одним приемником цель задачи максимального потока состоит в том, чтобы найти максимальный объем потока от источника к приемнику в сети. С 1950-х годов задача о максимальном потоке может использоваться для реальных ситуаций, таких как канализационные трубы и движение транспортных средств в городе. Алгоритм Форда-Фалкерсона впервые был создан для решения задачи о максимальном потоке. Когда задана потоковая сеть G с набором вершин V и ребер E, мы начинаем с f(u,v) = 0 для всех u,v, содержащихся в V, что дает начальный поток со значением 0. На каждой итерации поток значение увеличивается путем нахождения увеличивающего пути. Затем процесс повторяется до тех пор, пока не будет найден увеличивающий путь.На протяжении многих лет новые алгоритмы, такие как алгоритм блокирующего потока Диница и алгоритм максимального потока с принудительной переметкой, сделали решение задачи максимального потока намного более эффективным. В этом проекте мы рассмотрим эти алгоритмы, а также другие алгоритмы, используемые для решения задачи о максимальном потоке, и проанализируем, какие различия вызвали изменение эффективности.

Джеймс (Алекс) Паттон

Выводы дзета-функции

Ряды Диришле — это бесконечные ряды вида sum(a(n)/n^5, n=1. .infinity), когда a(n) является арифметической функцией. Заметим, что функция Римана-Дзета-ζ(s)-является рядом Диришеле с a(n)=1 для всех n. Свертка функций позволяет использовать полезную арифметику, включающую ряды Дирихле, которые Эммонс использовал вместе с логарифмическими производными для создания нового представления ζ (s). Умело определяя наши логарифмические производные, мы можем создать новые представления ζ(s) и показать их абсолютную сходимость.

Саммер Стинберг

Блоки и базы и BIBD, о боже!

Когда матроид представляет собой блочную конструкцию? Матроиды можно найти в математике, построенные из семейства независимых множеств, определенных на основном множестве.Они важны для нашего понимания комбинаторной оптимизации и связывают различные области дискретной математики. Блочные конструкции позволяют разделить набор разновидностей на разные группы, называемые блоками. Когда каждый блок не содержит всех элементов, все они имеют одинаковый размер, и каждая пара разновидностей появляется одинаковое количество раз, у нас есть BIBD (сбалансированный неполный блочный дизайн). Создавая категоризацию наборов на равные секции, блочные конструкции используются в практических исследованиях, таких как испытания шампуней и удобрений.В этом докладе мы исследуем, какие типы графических матроидов представляют собой блочные конструкции и какие свойства необходимы для этого. Когда основания матроида образуют блоки схемы? Есть ли другой способ связать их? Предварительные знания матроидов или блочных конструкций не требуются, просто интерес к некоторому графическому материалу!

Кэтрин Тардиф

Настоящее за пределами 15-головоломки

Головоломка 15 была объектом математических исследований более 100 лет.2-2)-Головоломка.

2010

Микаэла Балкус

Перемешайте свой способ заказа

Во все времена миллионы людей играли в карточные игры. Поскольку большинство карточных игр начинаются с колоды в случайном порядке, особый интерес вызывает метод перетасовки карт. В этом выступлении мы объясним и исследуем перетасовку «щипков», представленную в «Теории чисел» Джорджа Эндрюса. Наше основное внимание будет сосредоточено на следующем: сколько перетасовок требуется, чтобы вернуть определенную колоду карт в ее первоначальный порядок? Мы ответим на этот вопрос для колоды любого размера и продолжим дальше, обсудив верхнюю и нижнюю границы необходимого количества перетасовок, чтобы вернуть колоду в исходный порядок.

Стефани Лоури

Мозаика теорем Фибоначчи и обобщение теорем для включения M-омино

Распространенная детская игра — домино. Что, если вы хотите построить ряд длиной восемь дюймов, используя костяшки домино длиной два дюйма и квадраты длиной один дюйм? Сколькими различными способами вы могли бы соединить квадраты и костяшки домино, чтобы построить такой ряд? Мы начнем этот разговор с ответа на этот вопрос относительно чисел Фибоначчи. Затем мы рассмотрим некоторые известные теоремы, связанные с числами Фибоначчи, и обсудим, как можно использовать наши мозаики, чтобы понять, почему они верны.Затем эта идея расширяется с использованием m-мино, костяшек домино длины m, чтобы обобщить предыдущие результаты.

Коди Стейн

Измерение симметрии: отличительный номер

Что делает граф симметричным? Если граф можно вращать, отражать или каким-либо иным образом симметричен, то какие особые свойства он подразумевает? Различение графов — это процесс наблюдения за этими внутренними симметриями и присвоения раскраски вершинам таким образом, чтобы эти симметрии больше не существовали.Отличительное число графа, обозначаемое D(G), представляет собой минимальное количество цветов r, необходимое для различения графа G. Мы определяем алгоритм, который будет определять, различима ли определенная раскраска графа, путем систематического определения каждой подобная вершина и множество вершин различаются. С помощью этих свойств мы формально докажем отличительное число графа циклов Cn, графа-колеса Wn, полного графаKn, полного двудольного графа Kn,m и звездного графа Sn.Найден жадный алгоритм нахождения D(G) древовидного графа. Мы стремимся разработать или создать новый алгоритм, с помощью которого можно найти отличительное число более общего графа.

Крис Апшоу

Типы данных как математические объекты

Программисты используют типы данных для описания того, какие значения использует конкретная программа. Это позволяет компьютеру знать, как хранить эти значения и работать с ними. Исследуя эту практику математически, мы можем обнаружить интересные и полезные новые математические объекты и обнаружить, что некоторые знакомые идеи имеют гораздо более широкое применение, чем можно было бы подумать.К сожалению, введений в эту область очень мало. Я попытаюсь дать обзор основных идей и показать некоторые примеры результатов, к которым привело это исследование, в частности, показав, как выполнять алгебраические и математические вычисления с типами данных.

2009

Мариса Аллен

Глобальное потепление: математические расчеты, лежащие в основе моделирования климата

Глобальное потепление является спорной темой, отчасти потому, что сложные математические концепции, которые используются для объяснения этого явления, редко становятся доступными для широкой публики. В этом проекте мы исследуем математические и научные принципы, лежащие в основе моделей климата, в попытке демистифицировать глобальное потепление. В частности, мы рассмотрим уравнения, используемые в сложных климатических моделях, а также простое уравнение радиационного воздействия, используемое в общих климатических моделях (ОМК). Затем мы исследуем влияние повышения уровня CO2 на основные уравнения изменения климата.

Кристен Альмгрен

Перегородки: сколькими разными способами можно добраться до центра плюшевого ролла?

В этой презентации мы вводим идею разделов, а также производящие функции.Помня об этих идеях, мы рассмотрим множество примеров, чтобы дать краткое изложение методов, которые можно применять к разбиениям и производящим функциям. Имея в виду эти методы, мы представляем задачу, связанную с двумя наборами разделов. После изучения известного доказательства проблемы мы распространяем проблему на более общую постановку.

Джейкоб Арц

Счетные квадраты и домино: при чем здесь математика?

В то время как расположение костяшек домино и квадратов в различные узоры не обязательно является эзотерическим по своей природе, его применение в математике таково. Мы исследуем особый способ использования квадратов и костей домино, а именно с помощью мозаики.

Начнем с краткого рассмотрения последовательности Фибоначчи и ее комбинаторного представления. Мы показываем, что количество способов расставить костяшки и клетки на доске длины n равно n-му числу Фибоначчи. Из этого базового соотношения мы определяем ряд тождеств, включающих числа Фибоначчи, и стратегии для нахождения этих тождеств. Некоторые методы, которые мы используем, — это разбиение доски n-длины на разные части с учетом положения конкретной плитки и нахождение соответствий между двумя наборами плиток.

Мы также исследуем теорему Цекендорфа и ее приложение к комбинаторике и, в частности, к мозаике. Это позволяет нам дать явное определение для некоторых семейных тождеств Цекендорфов.

Бриттани Манжета

Раскраска списка и полиномы ладьи: использование шахмат для определения количества способов раскраски графа

Сколькими способами можно раскрасить карту? Сколькими способами можно расставить r ладей на шахматной доске mXn?

В теории графов мы раскрашиваем вершины графа таким образом, что если две вершины смежны, они окрашиваются по-разному. Раскраска списка — это ограничение этой раскраски, при котором не каждый цвет доступен для каждой вершины. Теперь мы назначаем каждой вершине список разрешенных цветов, в которые она может быть окрашена.

Ладейный многочлен — это производящая функция, представляющая количество способов, которыми мы можем разместить r неатакующих ладей на шахматной доске mXn, где неатакующая ладья — это такое размещение, при котором ни одна ладья не находится в одном столбце или строке с любой другой ладьей.

Мы связываем раскраску списков с полиномами ладей, преобразуя отношение между вершинами графа и соответствующим назначением списков в ладейную доску.Мы доказали, что полный граф G, имеющий допустимое списочное назначение, дает ладейный полином, старший коэффициент которого дает количество правильных раскрасок графа G. Мы продолжим этот результат, определив число правильных раскрасок графа G, если G не является завершить через включение.

Зак Гантенбейн

Математическое решето простых целых чисел Гаусса

Керенса Гимре

Ответ на животрепещущий вопрос: Анализ методов оценки остаточных запасов нефти и пиковой добычи нефти

Пик нефти (время, когда израсходована половина всей нефти, пригодной для эксплуатации) был введен в 1950-х годах М. Кинг Хабберт, который хотел предсказать время максимальной добычи нефти как для Соединенных Штатов, так и для всего мира. Точно следуя предсказанию Хабберта, пик добычи нефти в США пришелся на 1970-е годы. В настоящее время существует множество оценок времени пика добычи нефти в мире. Из-за огромных экономических последствий нехватки топлива пик масла является критической проблемой.

Мы изучаем методы оценки оставшихся объемов неиспользованных запасов нефти, в частности метод установления уровня.Метод набора уровней, разработанный в 1980-х годах, имеет множество применений в гидромеханике, материаловедении, компьютерном зрении, вычислительной геометрии, автоматизированном проектировании и обработке изображений. Путем численного решения уравнения Гамильтона-Якоби и применения соответствующей функции скорости, зависящей от кривизны (кривизна в данном случае зависит от интенсивности изображения), можно проанализировать изображение для устранения шума. Этот процесс помогает «очистить» сейсмическое изображение недр земли. Если эти изображения чище, можно найти более точные приближения для подземной нефти. Эта информация жизненно важна для нефтяных компаний при принятии решения об экономической эффективности бурения месторождения, а также важна при прогнозировании общего количества оставшейся подземной нефти.
В заключение мы оцениваем время пиковой добычи нефти, используя результаты метода установки уровня и анализируя популярный метод Хабберта.

Бобби Ларкинс

Размышление над прогнозами пути и боли мощных вращающихся затяжек, которые могут защитить население (ураганы)

Ураганы слишком долго убивали людей и разрушали места.Я, как бы ни хотел, не могу изменить этот факт. Улучшение системы, в которой люди
предупреждены, было следующим лучшим шагом, ограничивающим ущерб и спасающим жизни. В настоящее время общественность
предупреждена с помощью шкалы Саффира-Симпсона. Я буду сравнивать это с новой идеей
интегрированной кинетической энергии или IKE. Мы рассмотрим некоторые собранные необработанные данные,
посмотрим, как они генерируют значения IKE, и сделаем вывод о том, что метод
будет лучше для предупреждения общественности.

Стефани Мураяма

Действительно ли мир тесен? Исследование малых мировых сетей

Шесть степеней разделения — это теория, согласно которой всех разделяет не более шести человек. Вы можете не знать всех, но вы, вероятно, знаете кого-то, кто знает кого-то, кто знает этого человека. Что такое сеть малого мира? Маленькая мировая сеть — это тип социальной сети. Один из способов отобразить эту ситуацию — смоделировать сеть с помощью графа.

Графики социальных сетей на протяжении многих лет принимали различные формы.Иногда эти графики совершенно случайны, с мыслью, что любой человек в мире может знать любого другого человека в мире. В этом проекте мы рассматриваем более структурированные сети. Такие графы, как полные графы и граф с 1-решеткой, учитывают, что вероятность того, что вы будете знать своих соседей, выше, чем случайного человека. Например, полный граф может моделировать очень тесную группу друзей, где каждый в группе знает всех остальных в группе, в то время как 1-решетка может моделировать район, в котором человек знает своего соседа и соседа своего соседа, но не не знаю никого в округе. Конечно, ваш сосед может знать кого-то в другом городе, а этот человек может знать кого-то по всему миру, что делает его маленьким. Обратите внимание, что в структуре все еще есть немного случайности. Глядя на такие графики, мы можем исследовать как более традиционные, полностью случайные модели, так и более современные структурированные модели.

В этом проекте мы сосредоточимся на более структурированной модели с одной решеткой, созданной Уоттсом и Строгацем в 1998 году. Мы подробно исследуем этот граф, а также полный граф и некоторые другие модели.Какой график лучше всего моделирует реальную ситуацию? Мы исследуем различные свойства, такие как кластеризация и длина пути. Мы также пытаемся расширить производящие функции, чтобы помочь нам вычислить эти свойства.

Миган Поттер

Поломка! Обнаружение взаимосвязей между дизайнами и матроидами

Представленные в начале 1930-х годов теория дизайна и теория матроидов представляют собой две разные области дискретной математики. Они связаны? Как? Некоторые матроиды являются конструкциями; некоторые конструкции являются матроидами.2+n+1, n+1, 1)-схемы и все проективные геометрии являются матроидами.

Наиболее известным примером, связывающим планы и матроиды, является плоскость Фано, которая также является матроидом Фано и (7, 3, 1)-планом. Мы используем это, чтобы исследовать взаимосвязь между конкретными компонентами трех структур. Затем мы рассмотрим несколько разных классов матроидов — однородные, циклические, трансверсальные и т. д. — и разработаем метод перевода между матроидами и планами. Мы находим схемы с заданным матроидом и находим матроиды с заданной конструкцией.Можем ли мы обобщить это на весь класс матроидов? целый класс конструкций? Мы рассматриваем корреляции на этих конкретных примерах и стремимся сделать общие выводы о природе одной структуры из другой.

Марисса Уттерберг

Нестандартное мышление: последовательные варианты разделов

Мария Уолтерс

Заделка дыр в квазидеривациях

«Числовые производные» или «квазидеривации» $\Delta(x)$ впервые были упомянуты более 40 лет назад на конкурсе Патнэма как отображение от целых чисел к целым числам, которое удовлетворяло бы правилу произведения. {\Delta}(x)$ напоминает нашу стандартную производную f'(x) и во многих других случаях сильно различается.

2008

Карстен Гимре

Численный анализ нелинейных уравнений в частных производных, связанных с электрохимией

В этом проекте мы создали систему нелинейных дифференциальных уравнений в частных производных для моделирования электрохимической реакции. Наши результаты отвечают на давнюю гипотезу о том, зависит ли ток от определенного параметра реакции. После манипулирования областью задействованных функций мы могли решить их численно с помощью MATLAB.С помощью преобразований Лапласа мы смогли преобразовать систему уравнений в одно уравнение. Мы определили, что аналитическое решение уравнения кажется неизвестным и, вероятно, невозможным. Используя теоремы существования и единственности вместе с теоремой Лакса об эквивалентности, мы показали, что численное решение действительно является правильным решением.

Алексис Сакаида-Диас

Исследование влияния учебной программы, основанной на стандартах, на результаты теста AP-Calculus

Национальный совет учителей математики опубликовал стандарты преподавания математики детям от Pre-K до 12-го класса. Хотя стандарты кажутся разумными, до сих пор ведутся споры о том, приводят ли эти стандарты к надлежащему уровню обучения математике в начальной школе. В этом исследовании мы изучаем один показатель успеха стандартов, определяя, приводит ли основанная на стандартах учебная программа средней школы к более высоким баллам на экзамене AP-Calculus.

2007

Дейл Блем

Логарифмическое дифференцирование и метод Ньютона высшего порядка

Логарифмическая производная — это производная натурального логарифма функции D(ln(f(x)).Чаще всего это выражается как отношение f'(x)/f(x). Он используется в математике в области дифференциальных уравнений и теории чисел. Мы исследуем свойства логарифмической производной сначала строго как оператора, а затем в применении к методу Ньютона. Мы иллюстрируем модифицированный метод Ньютона, который использует логарифмическую производную более высокого порядка. Мы показываем как алгебраически, так и геометрически, что этот модифицированный метод Ньютона может сходиться быстрее, чем классический метод Ньютона.

Тара Фехтер

Исследование производной натурального числа с помощью логарифмической производной

Мы даем пояснительный обзор понятия производной натурального числа. Проиллюстрировано несколько примеров концепции. Мы связываем это понятие с логарифмической производной n’/n. Мы исследуем это понятие в незнакомой обстановке, функция, которая, на первый взгляд, не имеет различимой закономерности. Затем мы определяем предел средних значений этой логарифмической производной, ограничивая ее значения между двумя производящими функциями.

Мэтью Роуз

Вейвлеты и фильтры

Вейвлеты, представляющие собой локализованные волны, представляют собой замечательную новую альтернативу рядам Фурье для анализа математических сигналов. Некоторые новые приложения вейвлетов включают сжатие данных и извлечение признаков при обработке звука и изображений, включая новый стандарт JPEG2000. Мы специально исследуем вейвлет Хаара, который представляет собой импульс 1 и -1 в конечном диапазоне. Вейвлет Хаара — лишь один из многих вейвлетов, обладающих важным свойством ортогональности, и мы покажем, как это можно использовать для создания основы из набора вейвлетов.

2006

Хизер Хельмандоллар (LuBean)

Пути минимизации длины в гиперболической плоскости: доказательство с помощью парных субкалибровок

Доказательства минимизации с использованием парных калибровок в прошлом проводились с векторными полями нулевой дивергенции. В этой статье мы исследуем возможность использования векторных полей ненулевой дивергенции и их применения в парных калибровочных доказательствах в гиперболической плоскости. Мы рассмотрим задачу Штейнера с тремя и четырьмя точками, равномерно расположенными по окружности.

Тим Принс

Планирование бридж-клуба: пример дискретной оптимизации

Мы рассматриваем задачу составления расписания, которую в 1992 году поставил перед двумя математиками из Мичиганского университета местный бридж-клуб. Клуб хотел расписание, которое позволило бы каждому игроку играть против каждого игрока равное количество раз за их восемь ежегодных встреч. Чтобы найти такой график, мы сначала определяем его характеристики и определяем функцию, которая дает нам численное представление того, насколько данный график близок к оптимальному.Эта задача исследования операций плохо поддается линейному программированию, поэтому мы пробуем другие алгоритмы. Используя написанные нами компьютерные программы, мы пытаемся найти оптимальное расписание, используя несколько известных алгоритмов: полный перебор, жадный поиск, поиск наискорейшего спуска, поиск с отжигом и поиск с запретом. Используя жадный алгоритм, мы находим расписание, близкое к оптимальному, а оптимальные расписания находим с помощью наискорейшего спуска, отожженного поиска и табу-поиска. Мы также сравниваем время выполнения этих алгоритмов.

Калей Титкомб

Периодичность в динамических системах

Динамические системы возникают при изучении многих физических явлений, включая движение небесных тел, изменение погоды, рост и падение населения. Часто эти явления проявляют периодическое поведение: планеты и солнечные системы сохраняют довольно стабильные орбиты; температура и количество осадков отображают годовые модели; популяции хищников чередуются с популяциями жертв. Математика динамических систем помогает анализировать это периодическое поведение.В этом докладе мы исследуем теорию, гарантирующую в таких системах существование периодичности и позволяющую численно оценивать периодические точки. Мы применяем эту теорию к логистическому семейству функций, семейству, возникающему в динамике населения. Мы визуализируем динамику с помощью веб-диаграмм и бифуркационных диаграмм.

Старший проект

Биостатистика.  Студенты факультета биологии изучали влияние болезни Паркинсона на мозг мышей.Они исследовали мышей, инфицированных болезнью Паркинсона, и изучили изображения мозга. Делая это, они пытались вручную измерить плотность нервной ткани. Кимми работал над созданием компьютерной программы, которая будет анализировать изображение мозга мыши и вычислять для него плотность. Путем тщательного статистического анализа можно рассчитать точное измерение плотности мозга. Кимми также сравнила результаты своей программы с результатами, полученными отделом биологии, чтобы убедиться, что результаты максимально точны. Ученик: Кимми Симпкинсон. Советник: Гаррет Сондерс.

   Математика и физика. Изучая физику, Логан изучал различные разделы математики, имеющие приложения к физике. Проект начался с общего изучения топологии Манкреса, но в конечном итоге превратился в изучение тем, написанных физиком элементарных частиц. Некоторые из наиболее продвинутых тем, включая сопряжения векторных пространств и теорию гомологии. Цель состояла в том, чтобы лучше познакомиться с передовыми математическими темами, которые используют физики.Ученик: Логан Карпентер. Советник: Бен Вудрафф.

   Игровые стратегии. Использовал методы Монте-Карло для анализа и сравнения стратегий с играми. Этот проект включал в себя изучение того, как использовать объектно-ориентированное программирование в Python. Одной из конкретных игр была популярная карточная игра «Доминион», в которой сравнивались различные модификации стратегий кузницы и часовни. Ученик: Томас Брауэр. Советник: Бен Вудрафф.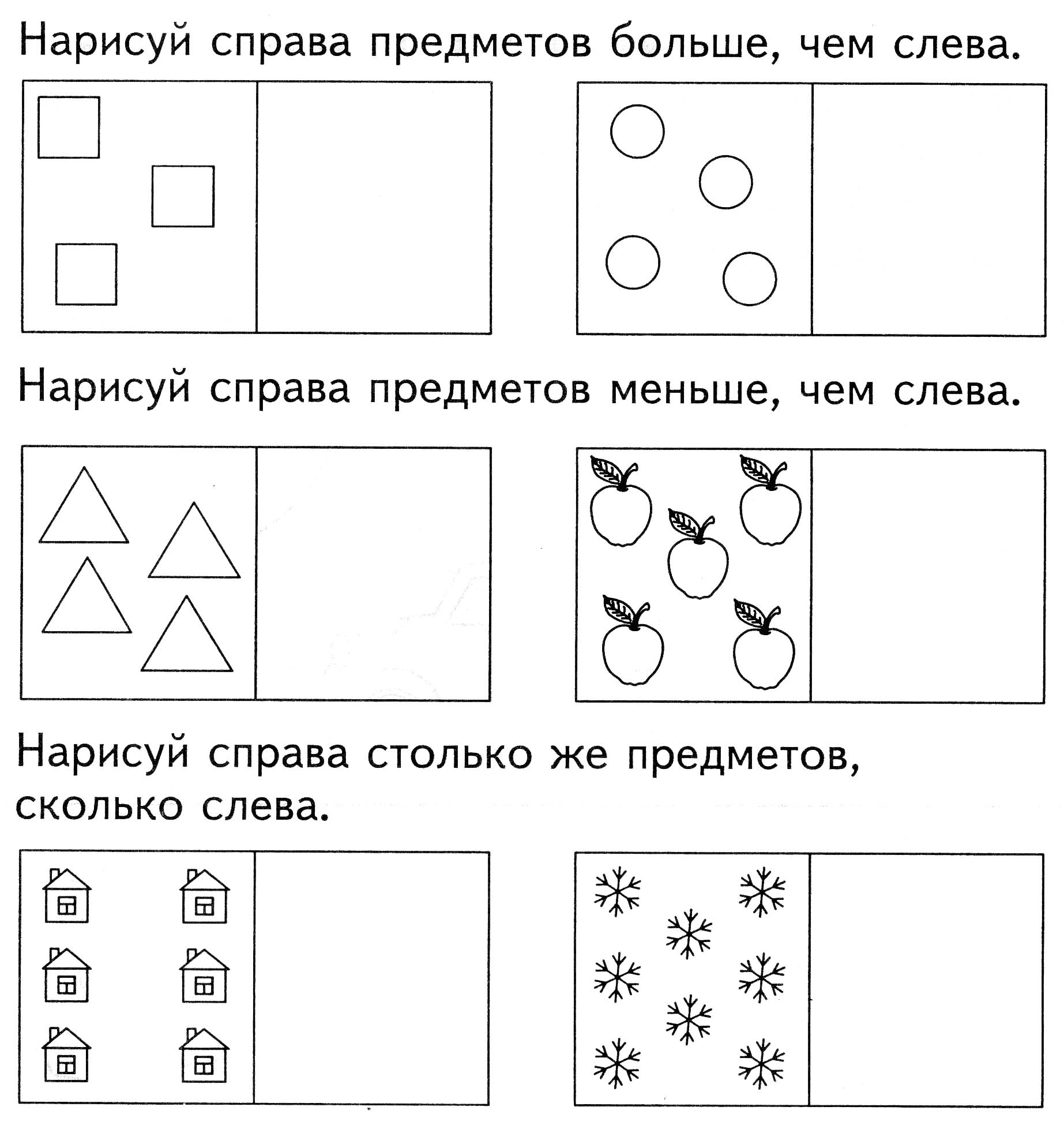

    Теория чисел и теория Галуа. При изучении введения в теорию чисел и теорию Галуа многие идеи были сосредоточены на неразрешимости квинтики.В конце концов, этот проект сосредоточился на обнаружении нескольких доказательств того, что симметрическая группа из 5 элементов является неразрешимой группой. Ученик: Маккей Виссер. Советник: Бен Вудрафф.

   Веб-разработка. Прошел большую часть наностепени Full Stack Web Developer через Udacity. См. Udacity.com для получения дополнительной информации. Ученик: Корбин Бакли. Советник: Бен Вудрафф.

   Планы размера статистической выборки. Разработал часть пакета R на основе моделей/инструментов в программном обеспечении Visual Sample Plan (vsp.pnnl.gov). Также просмотрела соответствующую литературу. Ученик: Томас Йохансен. Советник: Дж. Хэтэуэй.

   Комбинаторная матричная теория.  (0,1)-матричная задача. Изучил класс (0,1)-матриц, написал вычислительный код для реализации некоторых последних теорем в этой области и доказал теорему о мощности класса матриц.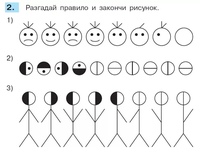 Также проанализирована соответствующая литература. Ученик: Маккей Виссер; Консультант: Кертис Нельсон

   Статистическое моделирование.  Выполнено статистическое моделирование для крупной молочной фермы в Южной Юте.Ученик: Джеффри Нильсон; Консультант: Крейг Джонсон

   Карта сохранения инвариантного визуального сходства и разделения (iVSSPM).  Этот проект был посвящен анализу видео с целью поиска объектов на видео. Например, предположим, что у вас есть сотни часов видеозаписи из аэропорта, и вы хотите знать, находился ли определенный человек в аэропорту во время наблюдения. Студенты: Митчелл Брейнхольт, Александр Дуглас и Стефани Нестор; Консультант: Ларри Чилтон

   Актуарий Подготовка к экзаменам.  Подготовлен к актуарному экзамену P (вероятность) и экзамену FM (финансовая математика). Этот проект лучше всего выполнять в группах. Ученики: Пирс Камстра, Крис Фицджеральд, Марк Миллер, Трэвис Лоэбс, Майкл Эсплин; Консультант: Ларри Чилтон

   Индивидуальное обучение.  В этом проекте делается попытка выявить учащихся из группы риска в начале семестра, чтобы обеспечить раннее вмешательство. Ученик: Карла Бруки; Консультант: Ларри Чилтон

   Трехмерный анализ облака точек. Специализированные камеры способны создавать облако точек объекта. Облако точек — это набор точек в трехмерном пространстве на поверхности объекта. Облако точек строится путем миллионов измерений расстояний от камеры до разных точек на поверхности объекта. Зная эти данные о расстоянии, можно создать точную 3D-модель поверхности объекта. К сожалению, когда эти модели создаются автоматически (без присмотра человека), они часто имеют дефекты.В этом проекте была предпринята попытка найти дыры (дефекты) в моделях, которых нет в моделируемом объекте. Существует множество приложений, включая промышленную безопасность, где инструменты удаленного контроля и моделирования позволяют компаниям выявлять потенциальные угрозы безопасности и риски. INL спонсировала этот проект. Ученик: Кэти Ларсон, Чжэнью Пан; Консультант: Ларри Чилтон

   Когерентная дифракционная рентгенография. Этот проект направлен на реконструкцию очень маленьких объектов на основе частичной информации, измеренной с помощью дифракционной картины/преобразования Фурье.Эллен изучала процесс формирования изображения и его связь с преобразованием Фурье. Wailam реализовал алгоритм поиска фазы Error Reduction. Остин реализовал два дополнительных алгоритма поиска фазы и сравнил их свойства. Ученики: Вайлам Чан, Эллен Дженсен, Остин Джонс; Советник: Ларри Чилтон

   Бизнес-аналитика.  Из-за того, что студенты поставили перед собой долгосрочную цель работать в области бизнес-аналитики, в этой отрасли были разработаны проекты. Оба студента в настоящее время работают в сфере бизнес-аналитики.Ученики: Роб Кларк, Трент Эдвалсон; Консультант: Ларри Чилтон

   Обратные задачи.  Кинси Кокс изучал свойства обратных задач, где задача состоит в том, чтобы определить свойства системы на основе наблюдений за системой. Она проиллюстрировала эти принципы несколькими примерами. Дэниел изучал, как идентифицировать радиоизотопы на основе их энергетического спектра гамма-излучения и истории времени гамма-распада. Ученики: Кинси Кокс, Дэниел Уоткинс; Советник: Ларри Чилтон

   Анализ временных рядов.  Проанализированы данные ФБР о преступлениях с использованием анализа временных рядов с помощью R. Студент: Остин Кеннеди; Консультант: Райан Кромар

   Математическая биология/моделирование. Пересмотрена стохастическая модель прогрессирования рака, чтобы включить новые функции роста. Ученик: Сара Тейлор; Консультант: Джейсон Роуз

   Методы статистического прогнозирования. Исследование прогнозов брекет-системы NCAA March Madness с использованием стандартных методов, а также оригинального подхода логистической регрессии. Ученик: Джастин Конвей; Советник: Гаррет Сондерс

   Комплексный анализ.  Изучал использование конформных отображений для моделирования различных физических явлений. Исследование было сосредоточено на моделировании воздушного потока с помощью преобразования Жуковского. Ученик: Лайла Барретт; Советник: Бонни Мун

   Топология.  Изучил форму пространства и другой текст, чтобы больше узнать о топологии и гиперболической геометрии. Ученик: Кристал Лоуренс; Советник: Бен Вудрафф

   Теория игр.  Изучил тему теории игр, основанную на студенческом опыте в области экономики.Ученик: Сэм Клайд; Консультант: Бен Вудрафф

   Абстрактная алгебра.  Изучал гомологическую алгебру, которая поможет в аспирантуре. Ученик: Тара Файф; Консультант: Бен Вудрафф

   Схемы шифрования.  Изучил схемы шифрования, которые помогут при подготовке к работе в АНБ или другой подобной работе. Ученик: Николас Лайнс; Консультант: Бен Вудрафф

Возможные области для старших проектов: Абстрактная алгебра, биостатистика, комбинаторика, комплексный анализ, дифференциальные уравнения, дифференциальная геометрия, дискретные динамические системы, динамические системы, обучение на основе запросов, линейная алгебра, машинное обучение, математическая биология/ Физиология, многомерное исчисление, дифференциальные уравнения с частными производными, статистика, случайные процессы, временные ряды, топология

5 советов по улучшению успеваемости учащихся по математике

Что нужно для повышения успеваемости учащихся и интереса к математике? Филадельфийское общество промышленной и прикладной математики (SIAM) запросило более 400 U. С. учителей математики средней школы за их советы, связанные с преподаванием и изучением математики.

«Хорошая новость заключается в том, что учащиеся могут добиться успеха на уроках математики при правильном настрое, отношении и поведении, независимо от естественной склонности или «хороших знаний по математике», — сказала Мишель Монтгомери, руководитель проекта MathWorks Math Modeling ( M3) Вызов в SIAM. «Использование количественных навыков для решения реальных открытых задач с использованием процесса математического моделирования — отличный способ начать работу.”

Все опрошенные учителя были тренерами студенческих команд, участвовавших в M3 Challenge, национальном интернет-соревновании без регистрации или платы за участие. Тысячи старшеклассников и старшеклассников проводят мартовские выходные, придумывая решение реальной проблемы с помощью математического моделирования. Чтобы добавить немного давления, когда студенты загружают задачу, у них есть только 14 часов, чтобы работать над ней. Мероприятие 2018 года стало 13-м ежегодным конкурсом.

Что рекомендуют учителя

1.Укрепляйте уверенность.  Более двух третей респондентов (68 процентов) назвали неуверенность в себе проблемой, которая мешает их ученикам добиться успехов в математике.

2. Поощряйте вопросы и оставляйте место для любопытства.  66% респондентов заявили, что их лучший совет для учащихся, стремящихся к успеху в математике, заключался в том, чтобы не только быть внимательными в классе, но и просить разъяснений, когда им нужно что-то лучше понять.

3.Делайте упор на концептуальное понимание, а не на процедуру.  Три из четырех респондентов (75 %) подчеркнули, что для достижения успеха необходимо усердно работать над пониманием математических понятий и моментов их применения, а не просто запоминать формулы.

4. Предлагайте аутентичные задачи, повышающие интерес учащихся к математике.  Шестьдесят три процента участников указали на желание, инициативу и мотивацию учащихся добиться успеха в математике как на критически важные, и большинство из них (80 процентов) заявили, что применение математики к реальным задачам помогает повысить как интерес учащихся, так и понимание .

5. Делитесь позитивным отношением к математике.  Учителя советуют родителям избегать негативных отзывов о математике и особенно не говорить, что это сложно или бесполезно (74 процента). Вместо этого они должны поощрять своих детей не сдаваться и помогать им найти наставников по математике, когда они ответить на вопросы (71%).

Неслучайно эти обучающие практики являются регулярной частью содействия математическому моделированию. С помощью моделирования учащиеся решают актуальные, аутентичные, реальные проблемы.По словам Лорен Таболински, менеджера академических программ в MathWorks, MathWorks спонсирует M3 Challenge, делая математику актуальной для студентов и карьеры.

Монтгомери из SIAM добавляет, что «неотъемлемыми элементами работы по моделированию являются такие вещи, как мотивация, идентификация переменных, влияющих на проблему (без подачи данных или подходов с ложечки), интуитивная проверка ответов и обоснование предлагаемых решений. Результат? Заинтересованность и энтузиазм в решении задачи, а также понимание того, что способность использовать навыки, имеющиеся в вашем наборе математических инструментов, может дать представление о важных проблемах, с которыми сегодня сталкиваются сообщества и мир.

Например, задача M3 Challenge 2018 года называлась «Лучше есть, чем никогда: сокращение пищевых отходов». Учащиеся рассмотрели вопрос, выявленный Продовольственной и сельскохозяйственной организацией Объединенных Наций: примерно одна треть всех продуктов питания, производимых в мире для потребления человеком, каждый год остается несъеденной.

В первой части задачи студенческие команды использовали математику, чтобы предсказать, смогут ли пищевые отходы в данном штате накормить всех живущих там людей, страдающих от нехватки продовольствия.Во второй части команды создали математическую модель, которую можно было использовать для определения количества пищевых отходов, которые домохозяйство производит за год, исходя из их особенностей и привычек. Им было предложено рассмотреть четыре различных типа домохозяйств.

Наконец, командам было предложено сделать предложения о том, как можно использовать выброшенную еду. Они использовали математическое моделирование, чтобы понять, какие стратегии следует использовать для перепрофилирования максимального количества пищи при минимальных затратах, и они учли затраты и выгоды, связанные с их стратегиями.

Поскольку такие задачи являются реалистичными, большими и запутанными, у студенческих команд есть много возможностей сделать реальный выбор в отношении того, как они хотят их решать, какие математические инструменты они будут применять для разработки и проверки своих моделей и как они будут общаться. их решение. Работы много, так что все члены команды могут внести свой вклад.

Если вы свяжете эту задачу моделирования M3 Challenge с приведенными выше советами тренеров-учителей, вы поймете, почему участие в соревнованиях по математическому моделированию в качестве командного вида спорта может помочь учащимся развить больше математической уверенности, компетентности и интереса.

Какой правильный объем домашнего задания?

Многие учителя и родители считают, что домашние задания помогают учащимся развивать учебные навыки и повторять понятия, полученные в классе. Другие считают домашнюю работу разрушительной и ненужной, что приводит к эмоциональному выгоранию и отказу детей от посещения школы. Десятилетия исследований показывают, что проблема более тонкая и сложная, чем думает большинство людей: домашняя работа полезна, но только до определенной степени. Больше всего выигрывают учащиеся старших классов, в то время как младшие дети выигрывают гораздо меньше.

Национальная родительская ассоциация и Национальная ассоциация образования поддерживают «рекомендацию по 10-минутным домашним заданиям» — 10-минутные домашние задания каждый вечер для каждого класса. Но многие учителя и родители сразу отмечают, что важно качество заданного домашнего задания и то, насколько оно соответствует потребностям учащихся, а не количество времени, затраченного на его выполнение.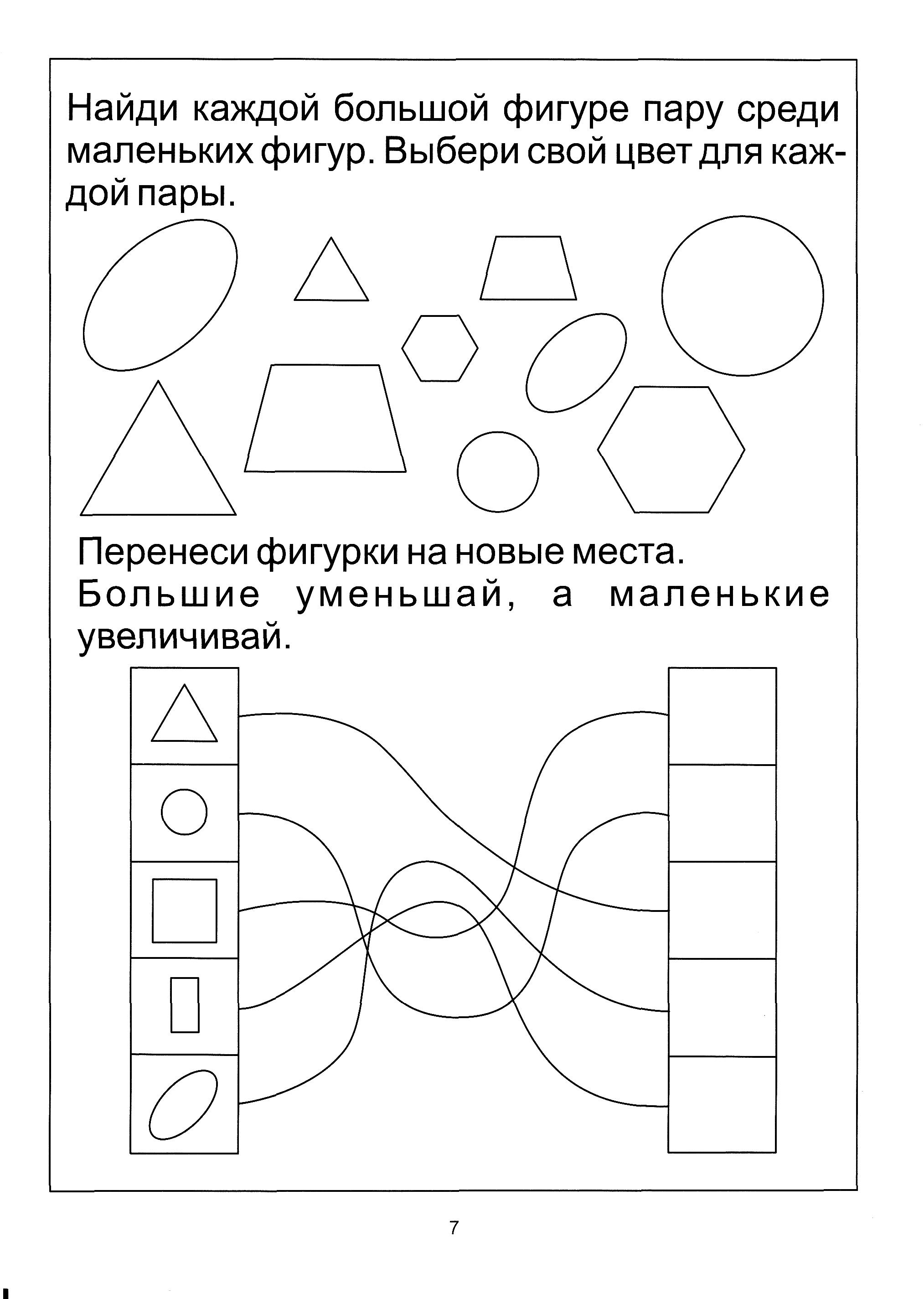

Руководство не учитывает учащихся, которым может потребоваться больше или меньше времени на выполнение заданий. В классе учителя могут вносить коррективы, чтобы поддержать учащихся, испытывающих затруднения, но дома задание, на выполнение которого у одного ученика уходит 30 минут, может занять у другого в два раза больше времени — часто по независящим от него причинам.А домашние задания могут увеличивать разрыв в успеваемости, ставя в невыгодное положение учащихся из малообеспеченных семей и учащихся с ограниченными возможностями обучения.

Тем не менее, 10-минутное правило полезно для установления предела: когда дети тратят слишком много времени на домашнее задание, нужно учитывать реальные последствия.

Небольшие пособия для учащихся начальной школы

Когда маленькие дети идут в школу, основное внимание следует уделять воспитанию любви к учебе, а слишком большое количество домашних заданий может подорвать эту цель.А молодые учащиеся часто не обладают навыками обучения, чтобы в полной мере извлечь пользу из домашних заданий, поэтому это может быть неэффективным использованием времени (Cooper, 1989; Cooper et al.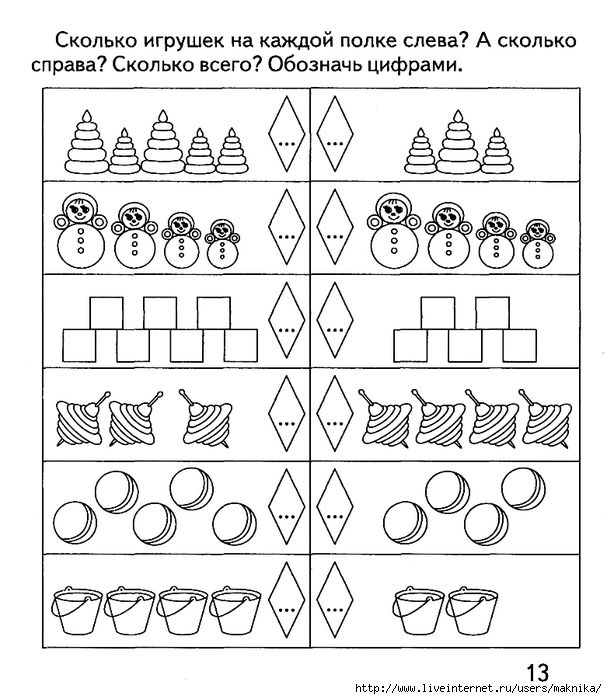 , 2006; Marzano & Pickering, 2007). Более эффективным занятием может быть вечернее чтение, особенно если в этом участвуют родители. Преимущества чтения очевидны: если учащиеся не умеют читать к концу третьего класса, у них меньше шансов добиться успехов в учебе и окончить среднюю школу (Fiester, 2013).

Для учительницы второго класса Жаклин Фиорентино небольшие преимущества домашних заданий не перевешивали потенциальный недостаток настроений маленьких детей против школы в раннем возрасте, поэтому она экспериментировала с отказом от обязательных домашних заданий.«Произошло нечто удивительное: они стали больше работать дома», — пишет Фиорентино. «Эта вдохновляющая группа 8-летних детей использовала свое новообретенное свободное время для изучения интересующих их предметов и тем». Она поощряла своих учеников читать дома и предлагала дополнительные домашние задания, чтобы продлить уроки в классе и помочь им повторить материал.

Умеренные льготы для учащихся средних школ

По мере того, как учащиеся взрослеют и развивают учебные навыки, необходимые для глубокого изучения темы и закрепления изученного, домашние задания также приносят им больше пользы. Ночные задания могут помочь им подготовиться к научной работе, и исследования показывают, что домашняя работа может принести умеренную пользу учащимся средней школы (Cooper et al., 2006). Недавние исследования также показывают, что онлайн-домашние задания по математике, которые могут быть адаптированы к уровню понимания учащихся, могут значительно повысить результаты тестов (Roschelle et al., 2016).

Однако слишком много заданий сопряжено с риском: исследование, проведенное в 2015 году, показало, что, когда учащимся средней школы уделялось более 90–100 минут ежедневного домашнего задания, их результаты тестов по математике и естественным наукам начали снижаться (Фернандес-Алонсо, Суарес-Альварес, и Муньис, 2015).Превышение этого верхнего предела может истощить мотивацию и внимание учащихся. Исследователи рекомендуют, чтобы «домашнее задание представляло определенный уровень сложности или сложности, но не настолько сложное, чтобы отбивать желание прилагать усилия». Учителя должны избегать не требующих больших усилий повторяющихся заданий и давать домашние задания «с целью привития рабочих привычек и поощрения автономного, самостоятельного обучения».

Другими словами, важно качество домашней работы, а не ее количество. Брайан Штабник, опытный учитель английского языка в средних и старших классах, предлагает учителям сделать шаг назад и задать себе следующие пять вопросов:

• Сколько времени это займет?
• Все ли учащиеся учтены?
• Будет ли задание способствовать будущему успеху?
• Поместит ли задание материал в контекст, недоступный классу?
• Предлагает ли задание поддержку в отсутствие учителя?

Больше преимуществ для старшеклассников, но и риски

К моменту поступления в старшую школу учащиеся должны быть уже на пути к тому, чтобы стать самостоятельными учениками, поэтому домашние задания действительно стимулируют обучение в этом возрасте, если они не являются чрезмерными (Cooper et al., 2006; Марцано и Пикеринг, 2007). Когда учащиеся тратят слишком много времени на домашнюю работу — более двух часов каждую ночь — они отнимают драгоценное время, чтобы отдохнуть и провести время с семьей и друзьями. Исследование, проведенное в 2013 году, показало, что у старшеклассников могут возникнуть серьезные проблемы с психическим и физическим здоровьем, от более высокого уровня стресса до лишения сна, когда им задают слишком много домашних заданий (Galloway, Conner, & Pope, 2013).

Домашнее задание в старшей школе всегда должно относиться к уроку и выполняться без посторонней помощи, а обратная связь должна быть четкой и четкой.

Учителя также должны иметь в виду, что не все учащиеся имеют равные возможности для выполнения домашнего задания дома, поэтому невыполненное домашнее задание может не быть истинным отражением их обучения — это может быть скорее результатом проблем, с которыми они сталкиваются вне школы. Им могут мешать такие проблемы, как отсутствие тихого уголка дома, такие ресурсы, как компьютер или широкополосное подключение, или родительская поддержка (OECD, 2014). В таких случаях ставить низкие оценки за домашнее задание может быть несправедливо.

Поскольку количество времени, обсуждаемое здесь, является общим, учителя средних и старших классов должны знать, сколько домашних заданий задают другие учителя. Может показаться разумным выделять 30 минут ежедневной домашней работы, но по шести предметам это три часа — намного больше разумного количества даже для старшеклассника. Психолог Морис Элиас считает это распространенной ошибкой: отдельные учителя устанавливают правила выполнения домашних заданий, которые в совокупности могут перегрузить учащихся. Он предлагает учителям работать вместе, чтобы разработать общешкольную политику домашних заданий и сделать ее ключевой темой вечера возвращения в школу и первых родительских собраний в этом учебном году.

Родители играют ключевую роль

Домашнее задание может быть мощным инструментом, помогающим родителям более активно участвовать в обучении своего ребенка (Walker et al., 2004). Это может дать представление о сильных сторонах и интересах ребенка, а также может побудить к разговорам о жизни ребенка в школе. Если родители положительно относятся к домашней работе, их дети, скорее всего, будут разделять те же ценности, способствуя успеху в учебе.

Но родители также могут быть властными, уделяя слишком много внимания результатам тестов или оценкам, что может быть разрушительным для детей (Madjar, Shklar, & Moshe, 2015).Родители должны избегать чрезмерного навязывания или контроля: учащиеся сообщают, что чувствуют меньшую мотивацию к учебе, когда у них нет достаточного пространства и самостоятельности для выполнения домашних заданий (Orkin, May, & Wolf, 2017; Patall, Cooper, & Robinson, 2008; Silinskas). и Кикас, 2017). Таким образом, хотя домашнее задание может побудить родителей больше заниматься своими детьми, важно не превращать его в источник конфликта.

Часть первая: Связь математики с работой и жизнью | Математика средней школы на работе: эссе и примеры для обучения всех учащихся

большая часть необходимых нам данных по Японии просто недоступна, потому что японский рынок менее развит, чем в США.S. Данные о водительских правах, данные о доходах, данные об образе жизни — все это обычное здесь и недоступное там. Американские ритейлеры до этого мало проникли в обе страны, поэтому у нас нет опыта, на который мы могли бы опереться. Мы все слышали, как трудно будет открыть торговые операции в Японии, но последние тенденции продаж среди продавцов компьютеров и продаж автозапчастей намекают на ослабление трудностей.

«План состоит в том, чтобы открывать три магазина в год, по 5000 квадратных футов каждый. Мы рассчитываем получать 700 долларов за квадратный фут, что более чем вдвое превышает опыт американских ритейлеров в США.с., но на 45% меньше, чем в наших магазинах. Кроме того, цены будут на 20% выше, чтобы компенсировать стоимость земли и зданий. Стоимость активов примерно в два раза выше, чем в США, но стоимость рабочей силы немного меньше. Пособия более тщательно покрываются государством. Конечно, есть большая неопределенность в объемах продаж, которые мы планируем. Ценообразование частично покроет неопределенность, но все же меньше, чем у товаров сопоставимого качества, уже предлагаемых в Японии.

«Позвольте мне перейти к соревнованиям и рассказать вам, что мы узнали.Мы установили долгосрочные отношения с 500 до 1000 семей в каждой стране. Это сопоставимо с нашей практикой в ​​США. Эти семьи не знают, что они работают именно с нашей компанией, так как это могло бы исказить их отчетность. Они держат нас в курсе своего каталога и опыта покупок, независимо от компании, в которой они покупают. Размер выборки достаточно велик, чтобы быть значимым, но, конечно, вы должны быть осторожны с небольшими различиями.

«Все семьи получают наш каталог и каталоги от нескольких наших конкурентов.Они соответствуют демографическому профилю образа жизни, дохода и образования людей, которых мы хотим видеть в качестве клиентов. Они являются опытными покупателями по каталогам, и это будет искажать их отзывы по сравнению с новыми покупателями по каталогам.

«Один из конкурентов присылает один 100-страничный каталог в квартал. Ассортимент довольно узкий — 200 товаров из 3000 отечественных. Они выбрали товары, которые вряд ли создадут проблемы с посадкой: в основном верхняя одежда и трикотажные рубашки, не много штанов, в основном мужские товары, не женские.Копия их каталога написана на кандзи, но, как нам сказали, стиль немного неестественный, вероятно, потому, что она была написана на английском и переведена, но нам нужно проверить эту гипотезу. Напротив, мы просто отправили им по почте тот же каталог, которым пользуемся в США, даже написанный на английском языке.

«Отклики покупателей были достаточно однозначными. Они предпочитают наш более широкий ассортимент в соотношении 3:1, хотя и не покупают большую часть товаров. увеличение продаж, видимо, потому, что им нравится смотреть каталог и проводить с ним больше времени.Опять же, нам нужны дополнительные испытания. Другая гипотеза заключается в том, что наша торговая марка просто более известна.

«Интересно, что они предпочитают нашу англоязычную версию, потому что им больше нравится читать каталог на другом языке.